AcWing 858. Prim算法求最小生成树
题目
给定一个 个点 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 ,其中 表示图中点的集合, 表示图中边的集合,,。
由 中的全部 个顶点和 中 条边构成的无向连通子图被称为 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 的最小生成树。
输入格式
第一行包含两个整数 和 。
接下来 行,每行包含三个整数 ,,,表示点 和点 之间存在一条权值为 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
,
,
图中涉及边的边权的绝对值均不超过 。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
思路
Prim 算法做的事情是:给定一个无向图,在图中选择若干条边把图的所有节点连起来。要求边长之和最小。在图论中,叫做求最小生成树。
Prim 算法采用的是一种贪心的策略。
每次将离连通部分的最近的点和点对应的边加入的连通部分,连通部分逐渐扩大,最后将整个图连通起来,并且边长之和最小。
我们将图中各个节点用数字 1 ~ n 编号。
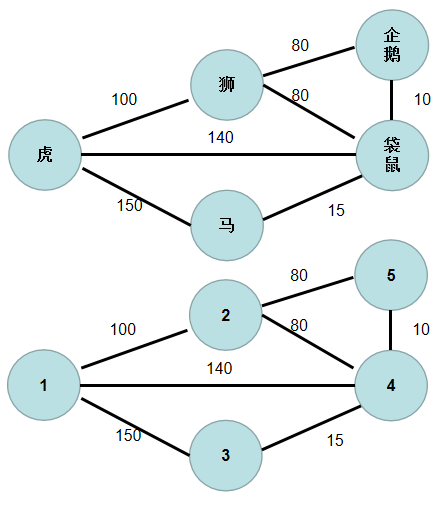
要将所有景点连通起来,并且边长之和最小,步骤如下:
-
步骤1
- 用一个
state数组表示节点是否已经连通。state[i]为真,表示已经连通,state[i]为假,表示还没有连通。初始时,state各个元素为假。即所有点还没有连通。 - 用一个
dist数组保存各个点到连通部分的最短距离,dist[i]表示i节点到连通部分的最短距离。初始时,dist数组的各个元素为无穷大。 - 用一个
pre数组保存节点的是和谁连通的。pre[i] = k表示节点i和节点k之间需要有一条边。初始时,pre的各个元素置为-1。
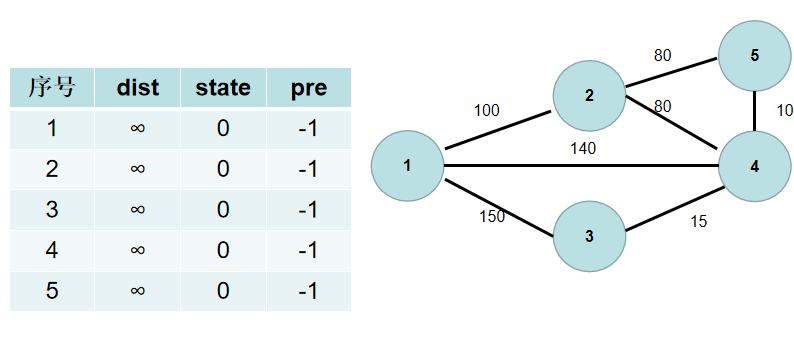
- 用一个
-
步骤2
- 从 1 号节点开始扩充连通的部分,所以 1 号节点与连通部分的最短距离为 0,即
dist[1]置为 0。
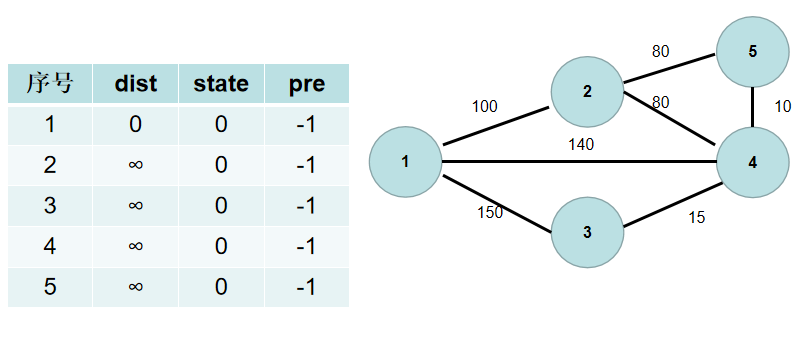
- 从 1 号节点开始扩充连通的部分,所以 1 号节点与连通部分的最短距离为 0,即
-
步骤3
- 遍历
dist数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 i。i节点就是下一个应该加入连通部分的节点,stata[i]置为 1。 - 用青色点表示还没有连通起来的点,红色点表示连通起来的点。
- 这里青色点中距离最小的是
dist[1],因此state[1]置为 1。

- 遍历
-
步骤4
- 遍历所有与 i 相连但没有加入到连通部分的点 j,如果 j 距离连通部分的距离大于
i、j之间的距离,即dist[j] > w[i][j](w[i][j]为i、j节点之间的距离),则更新dist[j]为w[i][j]。这时候表示,j 到连通部分的最短方式是和 i 相连,因此,更新pre[j] = i。 - 与节点 1 相连的有 2, 3, 4 号节点。1->2 的距离为 100,小于
dist[2],dist[2]更新为 100,pre[2]更新为1。1->4 的距离为 140,小于dist[4],dist[4]更新为 140,pre[2]更新为1。1->3 的距离为 150,小于dist[3],dist[3]更新为 150,pre[3]更新为1。
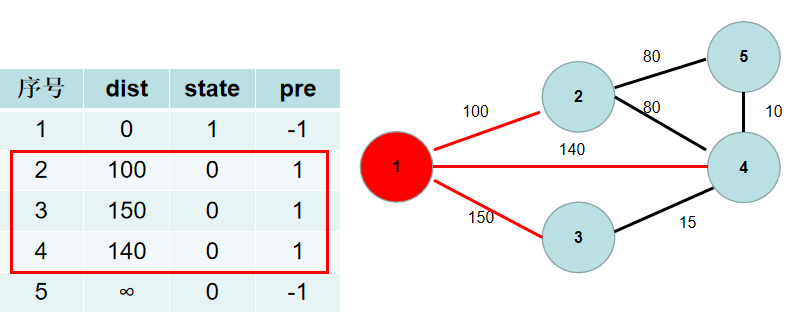
- 遍历所有与 i 相连但没有加入到连通部分的点 j,如果 j 距离连通部分的距离大于
-
步骤5
- 重复 3 4步骤,直到所有节点的状态都被置为 1.
- 这里青色点中距离最小的是
dist[2],因此state[2]置为 1。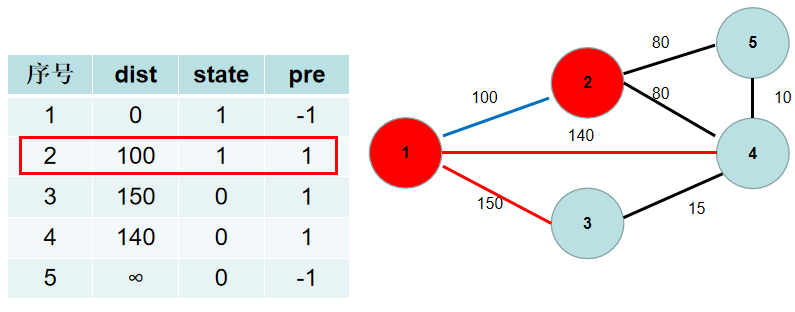
- 与节点 2 相连的有 5, 4号节点。2->5 的距离为 80,小于
dist[5],dist[5]更新为 80,pre[5]更新为 2。2->4 的距离为 80,小于dist[4],dist[4]更新为 80,pre[4]更新为2。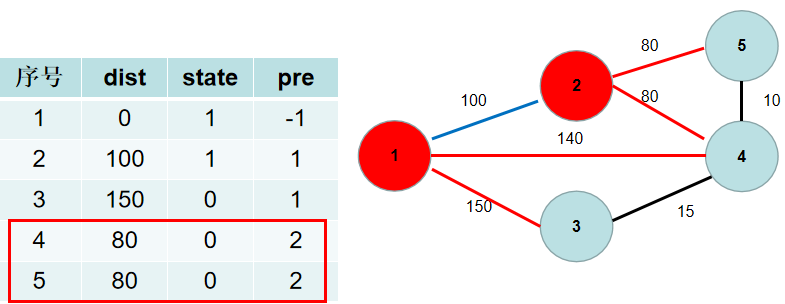
- 选
dist[4],更新dist[3],dist[5],pre[3],pre[5]。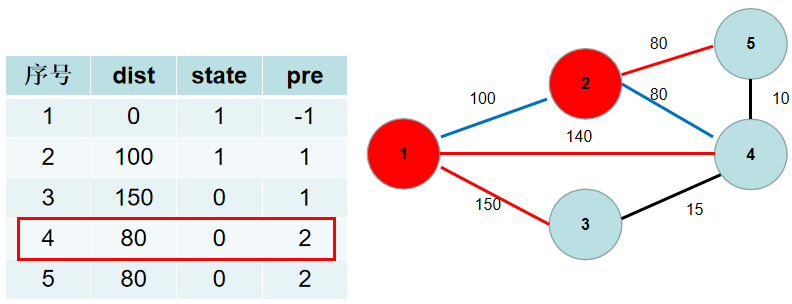
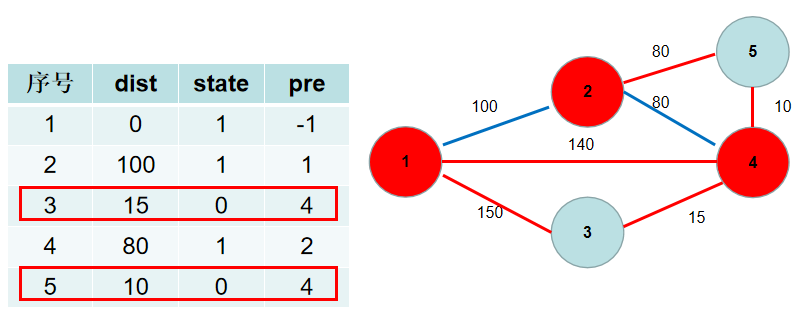
- 选
dist[5],没有可更新的。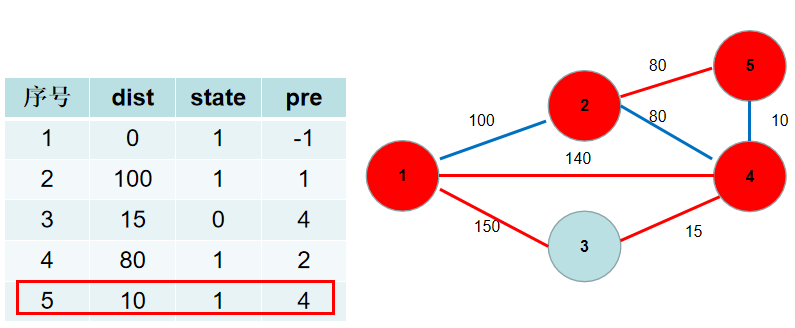
- 选
dist[3],没有可更新的。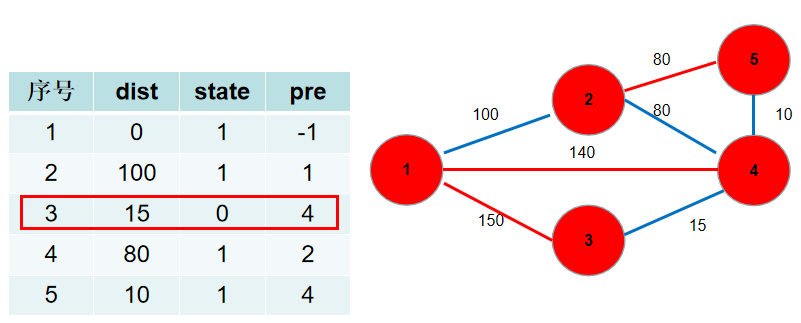
-
步骤6
- 此时
dist数组中保存了各个节点需要修的路长,加起来就是。pre数组中保存了需要选择的边。
- 此时
伪代码
int dist[n],state[n],pre[n];
dist[1] = 0;
for(i : 1 ~ n)
{
t <- 没有连通起来,但是距离连通部分最近的点;
state[t] = 1;
更新 dist 和 pre;
}
题解 - yxc版本
朴素版Prim算法,
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], dist[N];
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (dist[t] == INF) return INF;
st[t] = true;
res += dist[t];
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], g[t][j]);
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = g[b][a] = min(g[a][b], c);
}
int res = prim();
if (res == INF) puts("impossible");
else printf("%d\n", res);
return 0;
}
Kruskal算法
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010;
int n, m;
struct Edge
{
int a, b, c;
bool operator< (const Edge& t) const
{
return c < t.c;
}
}e[M];
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i ++ )
scanf("%d%d%d", &e[i].a, &e[i].b, &e[i].c);
sort(e, e + m);
for (int i = 1; i <= n; i ++ ) p[i] = i;
int res = 0, cnt = n;
for (int i = 0; i < m; i ++ )
{
int a = e[i].a, b = e[i].b, c = e[i].c;
if (find(a) != find(b))
{
res += c;
cnt -- ;
p[find(a)] = find(b);
}
}
if (cnt > 1) puts("impossible");
else printf("%d\n", res);
return 0;
}
yxc - baymin注释版本
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], dist[N]; // g[N][N]表示邻接矩阵 dist[i]表示节点i到连通部分的最短距离
bool st[N]; // st数组表示节点是否已经连通
int prim()
{
memset(dist, 0x3f, sizeof dist); // 初始化所有距离为无穷大
dist[1] = 0; // 1号节点与连通部分的最短距离为1
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1; // t 初始值置为-1 表示还没有找到符合条件(节点没有确定连通且距离连通部分最近)的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (dist[t] == INF) return INF;
st[t] = true;
res += dist[t];
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], g[t][j]);
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g); // 初始化邻接矩阵
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = g[b][a] = min(g[a][b], c); // 输入数据的同时直接赋值给邻接矩阵
}
int res = prim();
if (res == INF) puts("impossible"); // 如果res返回无穷大,则表示不存在,直接输出impossible
else printf("%d\n", res);
return 0;
}
其他人的版本
//2022.6.1 更新
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int g[N][N];//存储图
int dt[N];//存储各个节点到生成树的距离
int st[N];//节点是否被加入到生成树中
int pre[N];//节点的前去节点
int n, m;//n 个节点,m 条边
void prim()
{
memset(dt,0x3f, sizeof(dt));//初始化距离数组为一个很大的数(10亿左右)
int res= 0;
dt[1] = 0;//从 1 号节点开始生成
for(int i = 0; i < n; i++)//每次循环选出一个点加入到生成树
{
int t = -1;
for(int j = 1; j <= n; j++)//每个节点一次判断
{
if(!st[j] && (t == -1 || dt[j] < dt[t]))//如果没有在树中,且到树的距离最短,则选择该点
t = j;
}
//2022.6.1 发现测试用例加强后,需要判断孤立点了
//如果孤立点,直返输出不能,然后退出
if(dt[t] == 0x3f3f3f3f) {
cout << "impossible";
return;
}
st[t] = 1;// 选择该点
res += dt[t];
for(int i = 1; i <= n; i++)//更新生成树外的点到生成树的距离
{
if(dt[i] > g[t][i] && !st[i])//从 t 到节点 i 的距离小于原来距离,则更新。
{
dt[i] = g[t][i];//更新距离
pre[i] = t;//从 t 到 i 的距离更短,i 的前驱变为 t.
}
}
}
cout << res;
}
void getPath()//输出各个边
{
for(int i = n; i > 1; i--)//n 个节点,所以有 n-1 条边。
{
cout << i <<" " << pre[i] << " "<< endl;// i 是节点编号,pre[i] 是 i 节点的前驱节点。他们构成一条边。
}
}
int main()
{
memset(g, 0x3f, sizeof(g));//各个点之间的距离初始化成很大的数
cin >> n >> m;//输入节点数和边数
while(m --)
{
int a, b, w;
cin >> a >> b >> w;//输出边的两个顶点和权重
g[a][b] = g[b][a] = min(g[a][b],w);//存储权重
}
prim();//求最下生成树
//getPath();//输出路径
return 0;
}