AcWing 849. Dijkstra求最短路 I
题目
给定一个 个点 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 号点到 号点的最短距离,如果无法从 号点走到 号点,则输出 。
输入格式
第一行包含整数 和 。
接下来 行每行包含三个整数 ,,,表示存在一条从点 到点 的有向边,边长为 。
输出格式
输出一个整数,表示 号点到 号点的最短距离。
如果路径不存在,则输出 。
数据范围
,
,
图中涉及边长均不超过 。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路
Dijkstra 算法采用的是一种贪心的策略。
求源点到其余各点的最短距离步骤如下:
- 步骤1
- 用一个
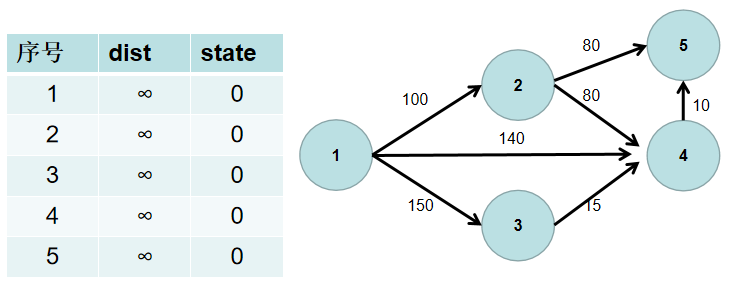
dist数组保存源点到其余各个节点的距离,dist[i]表示源点到节点i的距离。初始时,dist数组的各个元素为无穷大。 - 用一个状态数组
state记录是否找到了源点到该节点的最短距离,state[i]如果为真,则表示找到了源点到节点i的最短距离,state[i]如果为假,则表示源点到节点i的最短距离还没有找到。初始时,state各个元素为假。
- 用一个
- 步骤2
- 源点到源点的距离为 0。即
dist[1] = 0。
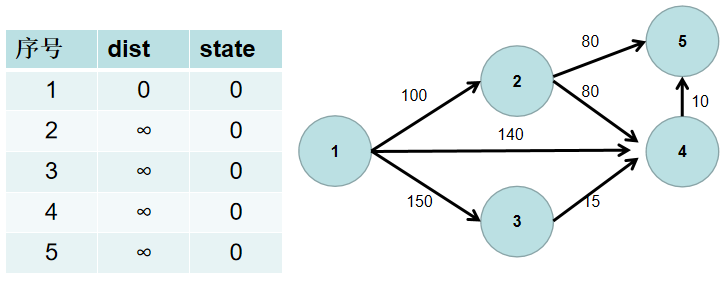
- 源点到源点的距离为 0。即
- 步骤3
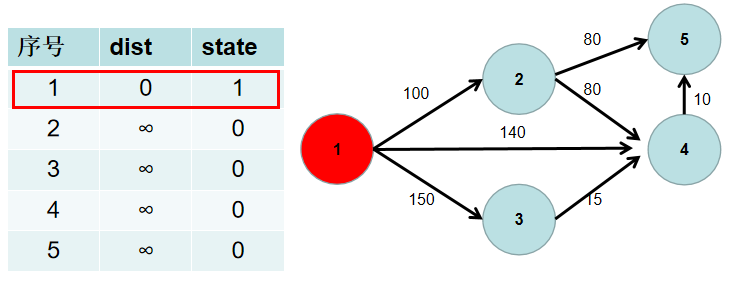
- 遍历
dist数组,找到一个节点,这个节点是:没有确定最短路径的节点中距离源点最近的点。假设该节点编号为i。此时就找到了源点到该节点的最短距离,state[i]置为 1。
- 遍历
- 步骤4
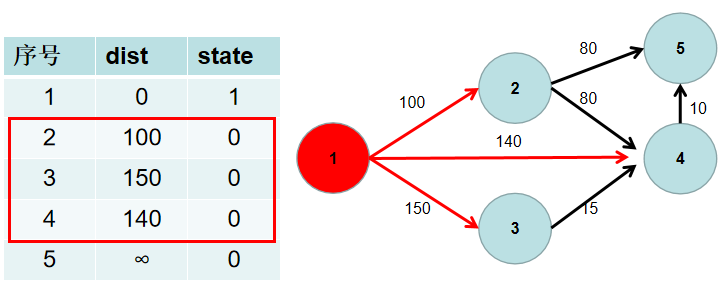
- 遍历 i 所有可以到达的节点 j,如果
dist[j]大于dist[i]加上 i -> j 的距离,即dist[j] > dist[i] + w[i][j](w[i][j]为 i -> j 的距离) ,则更新dist[j] = dist[i] + w[i][j]。
- 遍历 i 所有可以到达的节点 j,如果
- 步骤5
- 重复 3 4 步骤,直到所有节点的状态都被置为 1。
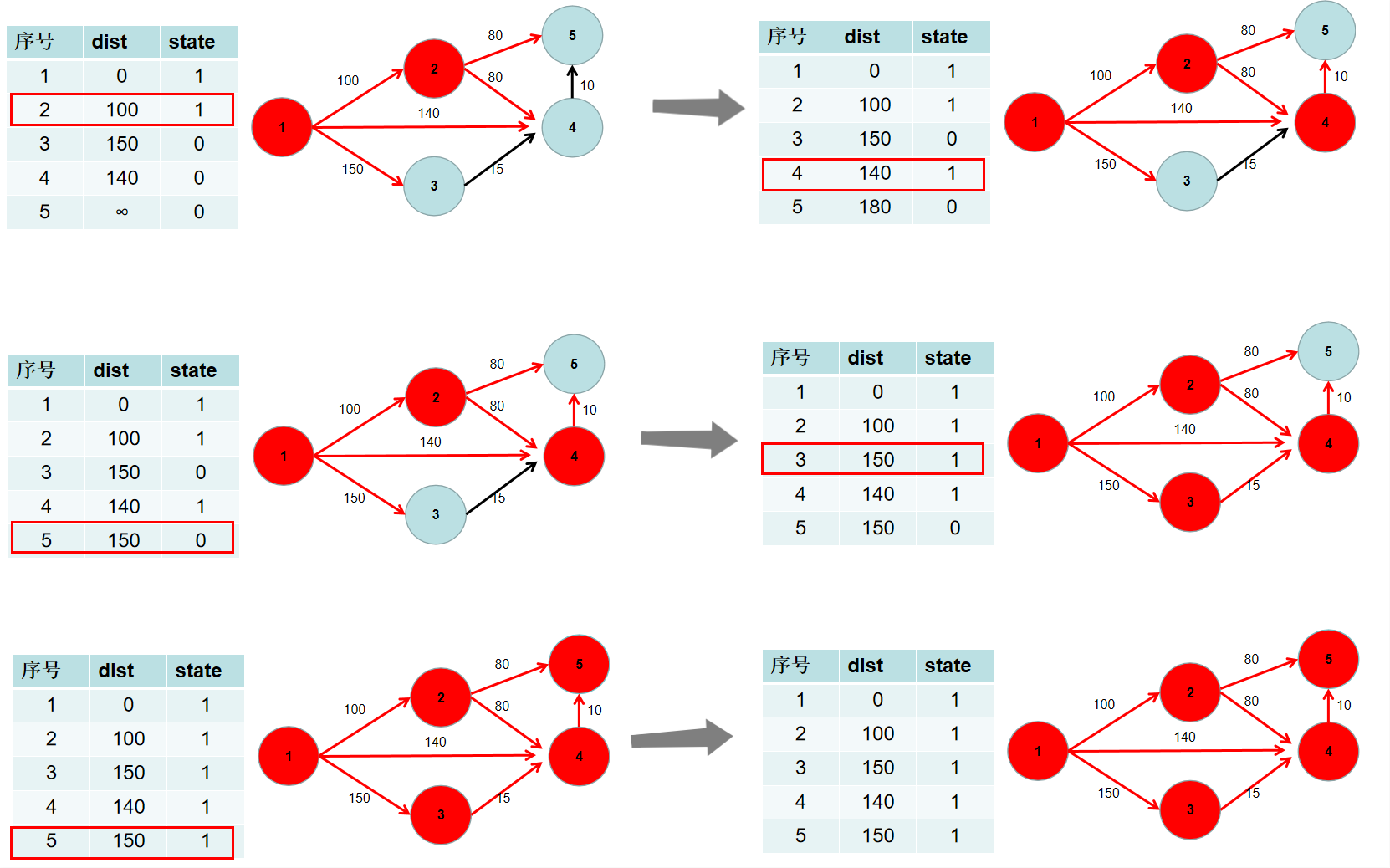
- 重复 3 4 步骤,直到所有节点的状态都被置为 1。
- 步骤6
- 此时
dist数组中,就保存了源点到其余各个节点的最短距离。
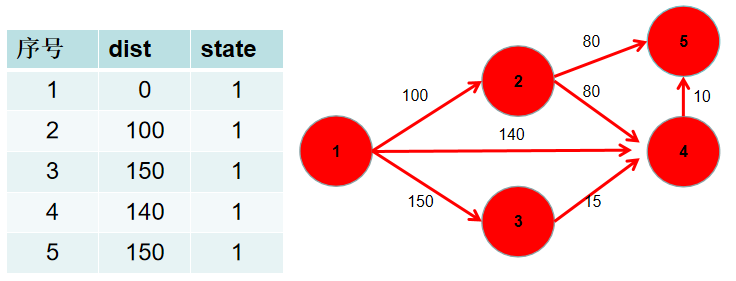
- 此时
伪代码
int dist[n],state[n];
dist[1] = 0, state[1] = 1;
for(i:1 ~ n)
{
t <- 没有确定最短路径的节点中距离源点最近的点;
state[t] = 1;
更新 dist;
}
题解 - yxc版本
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true;
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c);
}
int res = dijkstra();
if (res == INF) puts("-1");
else printf("%d\n", res);
return 0;
}
yxc - baymin注释版本
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], dist[N]; // g[N][N]表示邻接矩阵 dist[i]表示源点到节点i的距离
bool st[N]; // st 记录是否找到了源点到该节点的最短距离
int dijkstra()
{
memset(dist, 0x3f, sizeof dist); // 初始化距离为无穷大
dist[1] = 0; // 源点到源点的距离为 0
for (int i = 0; i < n; i ++ )
{
int t = -1; // t 初始值置为-1 表示还没有找到符合条件(没有确定最短路径且距离源点最近)的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j])) // 寻找 没有确定最短路径 且 距离源点最近 的点
t = j;
st[t] = true; // 标志位置为 true 表示该点的最短路径已找到 此时该点被记录在 t 中
for (int j = 1; j <= n; j ++ ) // 遍历 t 所有可以到达的节点 j
dist[j] = min(dist[j], dist[t] + g[t][j]); // 如果 dist[j] 大于 dist[t] 加上 t -> j 的距离变小则更新
}
return dist[n]; // 返回 1 号点到 n 号点的最短距离
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g); // 初始化邻接矩阵为无穷大
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c); // 随着输入的进行 立刻更新邻接矩阵的值
}
int res = dijkstra(); // 使用我们实现的 Dijkstra 算法将结果保存在res中
if (res == INF) puts("-1"); // 如果最终结果为无穷大 直接输出-1
else printf("%d\n", res);
return 0;
}
其他人的版本
#include<iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010;
int h[N], e[M], ne[M], w[M], idx;//邻接表存储图
int state[N];//state 记录是否找到了源点到该节点的最短距离
int dist[N];//dist 数组保存源点到其余各个节点的距离
int n, m;//图的节点个数和边数
void add(int a, int b, int c)//插入边
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void Dijkstra()
{
memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大
dist[1] = 0;//源点到源点的距离为置为 0
for (int i = 0; i < n; i++)
{
int t = -1;
for (int j = 1; j <= n; j++)//遍历 dist 数组,找到没有确定最短路径的节点中距离源点最近的点t
{
if (!state[j] && (t == -1 || dist[j] < dist[t]))
t = j;
}
state[t] = 1;//state[i] 置为 1。
for (int j = h[t]; j != -1; j = ne[j])//遍历 t 所有可以到达的节点 i
{
int i = e[j];
dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j]
}
}
}
int main()
{
memset(h, -1, sizeof(h));//邻接表初始化
cin >> n >> m;
while (m--)//读入 m 条边
{
int a, b, w;
cin >> a >> b >> w;
add(a, b, w);
}
Dijkstra();
if (dist[n] != 0x3f3f3f3f)//如果dist[n]被更新了,则存在路径
cout << dist[n];
else
cout << "-1";
}