AcWing 3786. 二叉排序树
题目
你需要写一种数据结构,来维护一些数,其中需要提供以下操作:
- 插入数值 。
- 删除数值 。
- 输出数值 的前驱(前驱定义为现有所有数中小于 的最大的数)。
- 输出数值 的后继(后继定义为现有所有数中大于 的最小的数)。
题目保证:
- 操作 1 插入的数值各不相同。
- 操作 2 删除的数值一定存在。
- 操作 3 和 4 的结果一定存在。
输入格式
第一行包含整数 ,表示共有 个操作命令。
接下来 行,每行包含两个整数 和 ,表示操作序号和操作数值。
输出格式
对于操作 , ,每行输出一个操作结果。
数据范围
,
输入样例:
6
1 1
1 3
1 5
3 4
2 3
4 2
输出样例:
3
5
思路
二叉排序树定义:
二叉排序树又称二叉搜索树。
二叉排序树为一棵空树,或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 左、右子树也分别为二叉排序树;
二叉排序树示例: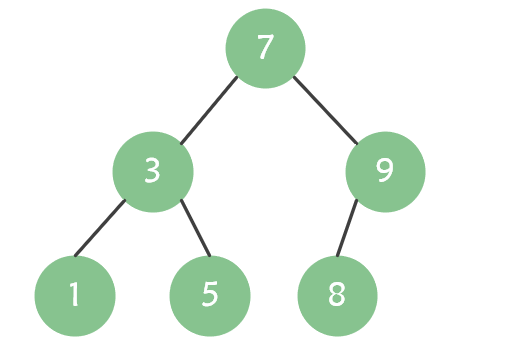
特殊的性质:二叉搜索树的中序遍历是一个有序序列。
【注】:没有键值相等的结点。
操作
-
插入操作:
- 从根节点出发,一直找到适合的位置为止
void insert(TreeNode* &root, int x) { if (!root) root = new TreeNode(x); else if (x < root->val) insert(root->left, x); else insert(root->right, x); } -
删除操作:
- 如果要删除的节点是
叶节点- 直接删除即可
- 图示:
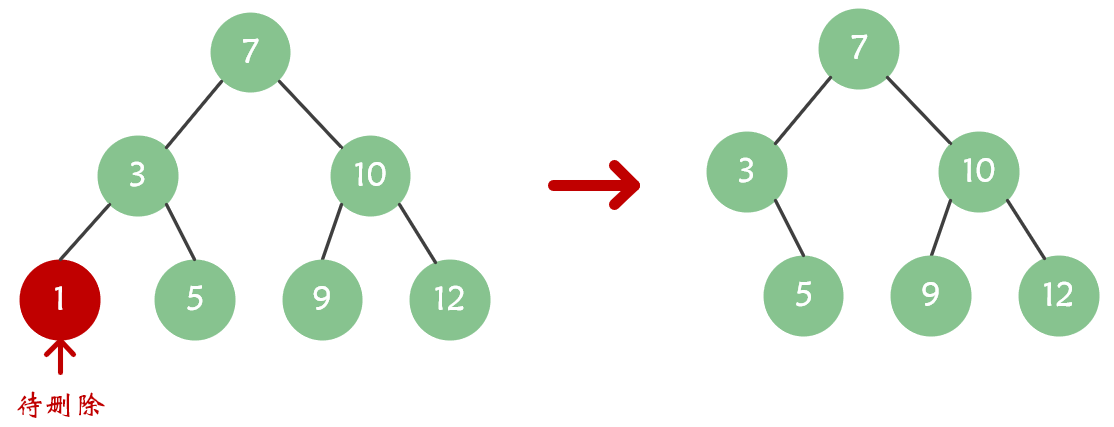
- 如果要删除的节点
仅有一个子树- 直接将子树根节点替换到删除结点的位置上
解释:直接用儿子结点替换删除结点是不会影响中序遍历有序性的。假设待删除结点只有左子树,则左子树上所有结点都是小于删除结点、大于或等于待删除结点的父结点的,因此用左子树的根替换待删除结点并不会破坏整棵树中序遍历的有序性。- 图示:
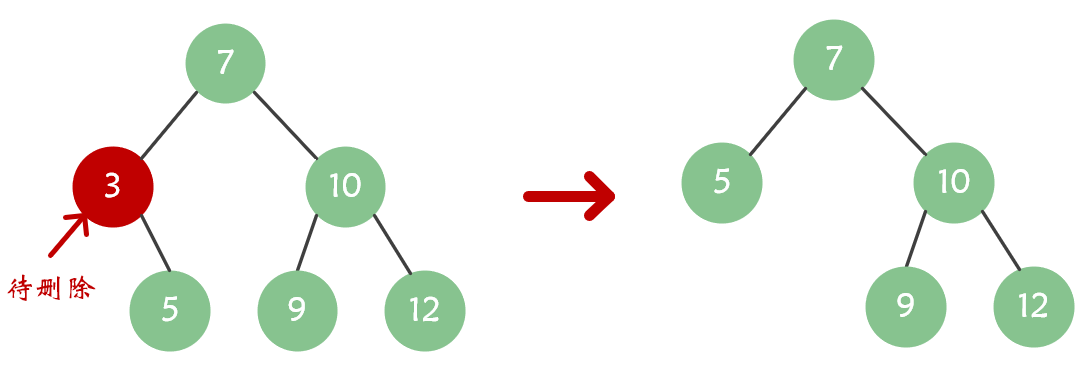
- 如果要删除的节点
同时拥有左右子树- 将待删除结点的
前驱结点(或后继结点)的值直接覆盖到待删除结点上,然后删除前驱结点(或后继结点)。这里的前驱结点是指“待删除结点的左子树中最大结点”,后继结点指的是“待删除结点右子树中最小结点”。 - 如果放在二叉搜索树中序遍历序列中,可以理解为下图(前驱结点的处理方法):

解释:如果目标节点有两个子树,则将目标节点的右子树中的最小的节点的信息拷贝至目标节点,然后将最小节点删除,即可实现删除目标节点(例如:目标节点为的值 3,它的右子树中最小节点的值为 4,则将目标节点的值修改为 4,然后删除最小节点即可)。- 图示(后继结点的处理方法):
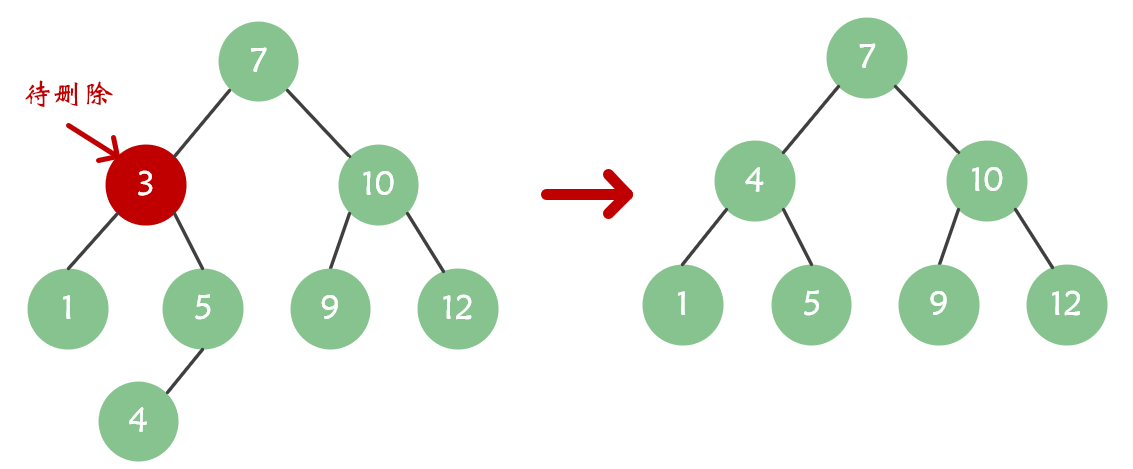
- 将待删除结点的
- 如果要删除的节点是
-
查找操作:
- 查询二叉搜索树中值为 的前驱/后继数值,即查询二叉搜索树中,比 大的第一个数,和比 小的第一个数。
int get_pre(TreeNode* root, int x) { if (!root) return -INF; if (root->val >= x) return get_pre(root->left, x); return max(root->val, get_pre(root->right, x)); } int get_suc(TreeNode* root, int x) { if (!root) return INF; if (root->val <= x) return get_suc(root->right, x); return min(root->val, get_suc(root->left, x)); }
题解
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int INF = 1e8;
struct TreeNode
{
int val;
TreeNode *left, *right;
TreeNode(int _val): val(_val), left(NULL), right(NULL) {}
}*root;
void insert(TreeNode* &root, int x)
{
if (!root) root = new TreeNode(x);
else if (x < root->val) insert(root->left, x);
else insert(root->right, x);
}
void remove(TreeNode* &root, int x)
{
if (!root) return;
if (x < root->val) remove(root->left, x);
else if (x > root->val) remove(root->right, x);
else
{
if (!root->left && !root->right) root = NULL;
else if (!root->left) root = root->right;
else if (!root->right) root = root->left;
else
{
auto p = root->left;
while (p->right) p = p->right;
root->val = p->val;
remove(root->left, p->val);
}
}
}
int get_pre(TreeNode* root, int x)
{
if (!root) return -INF;
if (root->val >= x) return get_pre(root->left, x);
return max(root->val, get_pre(root->right, x));
}
int get_suc(TreeNode* root, int x)
{
if (!root) return INF;
if (root->val <= x) return get_suc(root->right, x);
return min(root->val, get_suc(root->left, x));
}
int main()
{
int n;
cin >> n;
while (n -- )
{
int t, x;
cin >> t >> x;
if (t == 1) insert(root, x);
else if (t == 2) remove(root, x);
else if (t == 3) cout << get_pre(root, x) << endl;
else cout << get_suc(root, x) << endl;
}
return 0;
}