AcWing 3765. 表达式树

题目

请设计一个算法，将给定的表达式树(二叉树)转换为等价的中缀表达式(通过括号反映操作符的计算次序)并输出。

例如，当下列两棵表达式树作为算法的输入时：

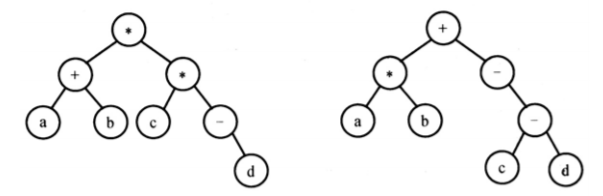
输出的等价中缀表达式分别为 (a+b)*(c*(-d)) 和 (a*b)+(-(c-d))。

注意：

• 树中至少包含一个运算符。
• 当运算符是负号时，左儿子为空，右儿子为需要取反的表达式。
• 树中所有叶节点的值均为非负整数。

样例：

输入：二叉树[+, 12, *, null, null, 6, 4, null, null, null, null]如下图所示：
    +
   / \
  12  *
     / \
    6   4

输出：12+(6*4)

数据范围
给定二叉树的非空结点数量保证不超过 $1000$。
给定二叉树保证能够转化为合法的中缀表达式。

思路

表达式树
表达式树的叶节点是操作数，其他节点是操作符

注意
由题目可知，本题我们需要假设所有运算符优先级相同，只能使用括号来表示优先级的高低

思路
求一棵表达式树的中缀表达式其实就是求这棵树的中序遍历，只是需要额外加上括号。
所以我们只需要写出中序遍历即可(需要将括号将子树括起来，最外层不需要括号)

关于时间复杂度
由于在C++中return string类型时，每次返回都需要复制一遍整个string，所以函数return $n$ 次需要进行 $1+2+…+n$，大约为 $O(n^2)$ 级别的时间复杂度。
我们可以通过定义一个全局变量ans，让函数不再每次都return，而是直接通过字符串拼接的方式，这样就将时间复杂度降为了 $O(n)$ 级别。

题解

$O(n^2)$ 写法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     string val；
 *     TreeNode *left;
 *     TreeNode *right;
 * };
 */
class Solution {
public:
    string dfs(TreeNode* root) {
        if (!root) return "";
        if (!root->left && !root->right) return root->val;
        return '(' + dfs(root->left) + root->val + dfs(root->right) + ')';
    }

    string expressionTree(TreeNode* root) {
        return dfs(root->left) + root->val + dfs(root->right);
    }
};

$O(n)$ 写法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     string val；
 *     TreeNode *left;
 *     TreeNode *right;
 * };
 */
class Solution {
public:
    string ans;

    void dfs(TreeNode* root) {
        if (!root) return;
        if (!root->left && !root->right) ans += root->val;
        else
        {
            ans += '(';
            dfs(root->left);
            ans += root->val;
            dfs(root->right);
            ans += ')';
        }
    }

    string expressionTree(TreeNode* root) {
        dfs(root->left), ans += root->val, dfs(root->right);
        return ans;
    }
};