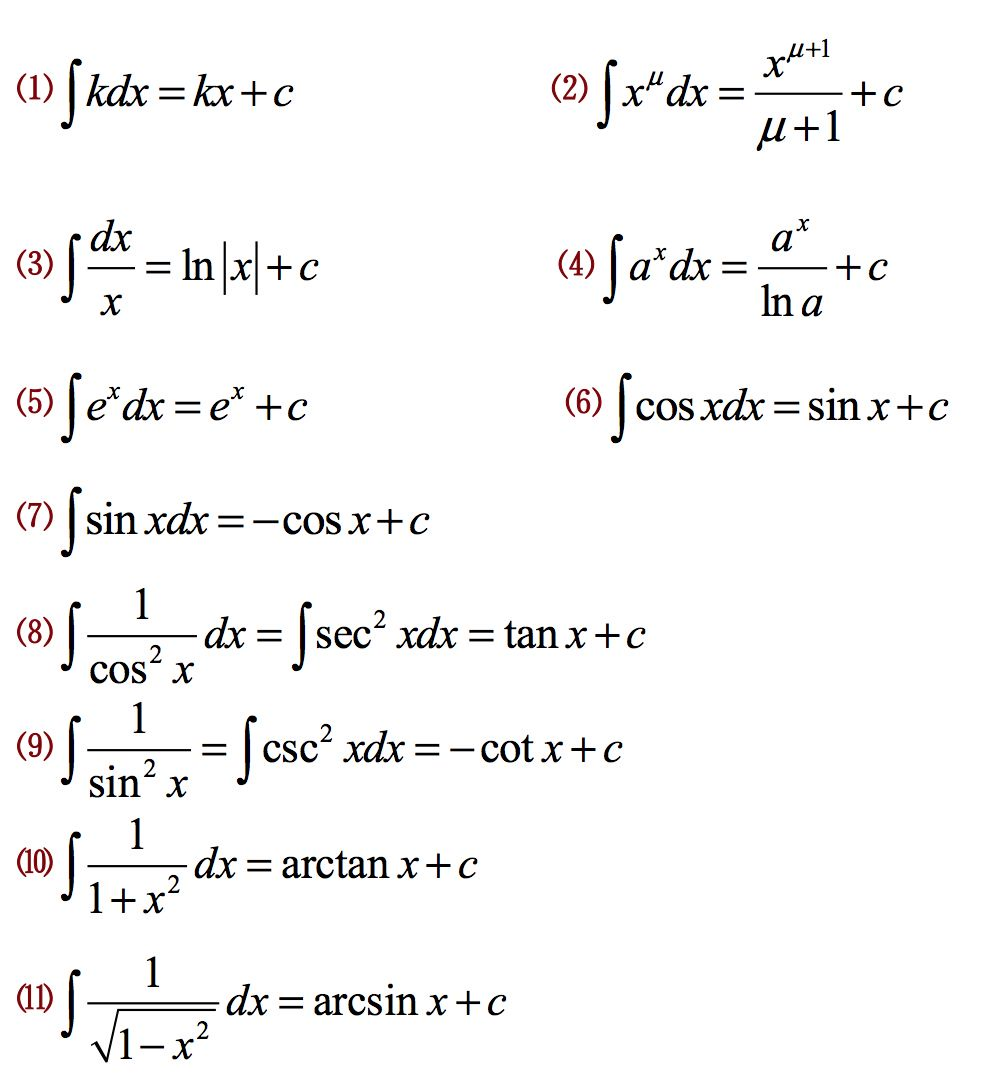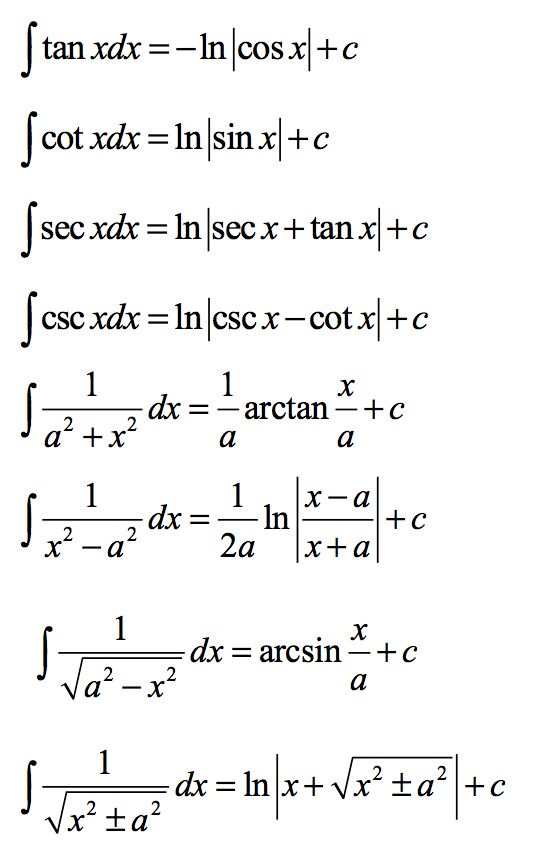高数公式速查

数学
222

立方差 / 立方和公式

a3−b3=(a−b)(a2+ab+b2)a^3-b^3=(a-b)(a^2+ab+b^2)
a3+b3=(a+b)(a2−ab+b2)a^3+b^3=(a+b)(a^2-ab+b^2)

排列组合

Anm=n(n−1)(n−2)⋯(n−m+1)=n!(n−m)!A^m_n=n(n-1)(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!}
Cnm=Anmm!=n!m!(n−m)!C^m_n=\frac{A^m_n}{m!}=\frac{n!}{m!(n-m)!}
Cnm=Cnn−mC^m_n=C^{n-m}_n其中 n≥mn≥m

等差、等比数列公式

等差数列：
an−an−1=d(n≥2，n∈N+)a_n-a_{n-1}=d(n≥2，n∈N^+)
an=a1+(n−1)d=am+(n−m)da_n=a_1+(n-1)d=a_m+(n-m)d
Sn=na1+n(n−1)2d=n(a1+an)2S_n=na_1+\frac{n(n-1)}{2}d=\frac{n(a_1+a_n)}{2}
等比数列：
an+1an=q(an≠0)\frac{a_{n+1}}{a_{n}}=q(a_{n}≠0)
an=a1qn−1=amqn−ma_n=a_1q^{n-1}=a_mq^{n-m}
Sn=a1(1−qn)1−q=a1−anq1−qS_n=\frac{a_1(1-q^n)}{1-q}=\frac{a_1-a_nq}{1-q}

三角函数

正割sec⁡x=1cos⁡x\sec x=\frac{1}{\cos x}
余割csc⁡x=1sin⁡x\csc x=\frac{1}{\sin x}
余切cot⁡x=1tan⁡x\cot x=\frac{1}{\tan x}
tan⁡2x+1=sec⁡2x\tan ^2 x +1=\sec ^2 x
sin⁡(−α)=−sin⁡α\sin(-\alpha)=-\sin\alpha，cos⁡(−α)=cos⁡α\cos(-\alpha)=\cos\alpha，tan⁡(−α)=−tan⁡α\tan(-\alpha)=-\tan\alpha，cot⁡(−α)=−cot⁡α\cot(-\alpha)=-\cot\alpha
sin⁡(π−α)=sin⁡α\sin(\pi-\alpha)=\sin\alpha，cos⁡(π−α)=−cos⁡α\cos(\pi-\alpha)=-\cos\alpha，tan⁡(π−α)=−tan⁡α\tan(\pi-\alpha)=-\tan\alpha，cot⁡(π−α)=−cot⁡α\cot(\pi-\alpha)=-\cot\alpha
sin⁡(2π−α)=−sin⁡α\sin(2\pi-\alpha)=-\sin\alpha，cos⁡(2π−α)=cos⁡α\cos(2\pi-\alpha)=\cos\alpha，tan⁡(2π−α)=−tan⁡α\tan(2\pi-\alpha)=-\tan\alpha，cot⁡(2π−α)=−cot⁡α\cot(2\pi-\alpha)=-\cot\alpha
sin⁡(π2+α)=cos⁡α\sin(\cfrac{π}{2}+\alpha)=\cos\alpha，sin⁡(π2−α)=cos⁡α\sin(\cfrac{π}{2}-\alpha)=\cos\alpha，cos⁡(π2+α)=−sin⁡α\cos(\cfrac{π}{2}+\alpha)=-\sin\alpha，cos⁡(π2−α)=sin⁡α\cos(\cfrac{π}{2}-\alpha)=\sin\alpha
tan⁡(π2+α)=−cot⁡α\tan(\cfrac{π}{2}+\alpha)=-\cot\alpha，tan⁡(π2−α)=cot⁡α\tan(\cfrac{π}{2}-\alpha)=\cot\alpha，cot⁡(π2+α)=−tan⁡α\cot(\cfrac{π}{2}+\alpha)=-\tan\alpha，cot⁡(π2−α)=tan⁡α\cot(\cfrac{π}{2}-\alpha)=\tan\alpha
和差化积巧记：
帅+帅=帅哥：
sin⁡α+sin⁡β=2sin⁡α+β2cos⁡α−β2\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}
帅-帅=哥帅：
sin⁡α−sin⁡β=2cos⁡α+β2sin⁡α−β2\sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
哥+哥=哥哥：
cos⁡α+cos⁡β=2cos⁡α+β2cos⁡α−β2\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}
哥-哥=负嫂嫂：
cos⁡α−cos⁡β=−2sin⁡α+β2sin⁡α−β2\cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
积化和差即为和差化积倒过来：
帅哥=帅+帅：
sin⁡αcos⁡β=12[sin⁡(α+β)+sin⁡(α−β)]\sin\alpha\cos\beta=\frac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)]
哥帅=帅-帅：
cos⁡αsin⁡β=12[sin⁡(α+β)−sin⁡(α−β)]\cos\alpha\sin\beta=\frac{1}{2}[\sin(\alpha+\beta)-\sin(\alpha-\beta)]
哥哥=哥+哥：
cos⁡αcos⁡β=12[cos⁡(α+β)+cos⁡(α−β)]\cos\alpha\cos\beta=\frac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)]
负嫂嫂=哥-哥：
sin⁡αsin⁡β=−12[cos⁡(α+β)−cos⁡(α−β)]\sin\alpha\sin\beta=-\frac{1}{2}[\cos(\alpha+\beta)-\cos(\alpha-\beta)]

奇变偶不变，符号看象限
sin⁡(nπ2+α)={(−1)n2sin⁡α(n为偶数)(−1)n−12cos⁡α(n为奇数)\sin(\cfrac{n\pi}{2}+\alpha) = \begin{cases} (-1)^{\frac{n}{2}}\sin\alpha(n为偶数)\\(-1)^{\frac{n-1}{2}}\cos\alpha(n为奇数)\end{cases}

cos⁡(nπ2+α)={(−1)n2cos⁡α(n为偶数)(−1)n+12sin⁡α(n为奇数)\cos(\cfrac{n\pi}{2}+\alpha) = \begin{cases} (-1)^{\frac{n}{2}}\cos\alpha(n为偶数)\\(-1)^{\frac{n+1}{2}}\sin\alpha(n为奇数)\end{cases}

等价无穷小

当x→0x→0时，sin⁡x∼x\sin x\sim x，tan⁡x∼x\tan x\sim x，ln⁡(1+x)∼x\ln(1+x)\sim x，ex−1∼xe^x-1\sim x，ax−1∼xln⁡aa^x-1\sim x\ln a，1−cos⁡x∼12x21-\cos x\sim \frac{1}{2}x^2，1+xn−1∼1nx\sqrt[n]{1+x}-1\sim \frac{1}{n}x，(1+x)a−1∼ax(a≠0)(1+x)^a-1\sim ax(a≠0)，arcsin⁡x∼x\arcsin x\sim x，arctan⁡x∼x\arctan x\sim x

幂指函数转化

f(x)g(x)=eg(x)ln⁡f(x)f(x)^{g(x)}=e^{g(x)\ln f(x)}

常用结论

1∞型极限：1^∞型极限：lim⁡x→∞(1+ax)bx+c=eab\lim \limits_{x \to \infty}(1+\frac{a}{x})^{bx+c}=e^{ab}

利用夹逼准则可以证得以下结论
lim⁡n→∞a1n+a2n+⋯+amnn=a\lim\limits_{n\rightarrow\infty}\sqrt[n]{a^n_1+a^n_2+\cdots +a^n_m}=a其中，a=max⁡{ai}a=\max\{a_i\}

间断点

分类{第一类间断点：lim⁡x→x0−f(x)，lim⁡x→x0+f(x)都存在.第二类间断点：lim⁡x→x0−f(x)，lim⁡x→x0+f(x)至少有一个不存在.分类\begin{cases} 第一类间断点：\\\qquad\lim\limits_{x\rightarrow x^-_0}f(x)，\lim\limits_{x\rightarrow x^+_0}f(x)都存在.\\第二类间断点：\\\qquad\lim\limits_{x\rightarrow x^-_0}f(x)，\lim\limits_{x\rightarrow x^+_0}f(x)至少有一个不存在.\end{cases}

第一类{可去型间断点：lim⁡x→x0−f(x)=lim⁡x→x0+f(x){≠f(x0)f(x0)无定义跳跃型间断点：lim⁡x→x0−f(x)≠lim⁡x→x0+f(x)第一类\begin{cases} 可去型间断点：\\\qquad\lim\limits_{x\rightarrow x^-_0}f(x)=\lim\limits_{x\rightarrow x^+_0}f(x)\begin{cases} ≠f(x_0)\\f(x_0)无定义\end{cases}\\跳跃型间断点：\\\qquad\lim\limits_{x\rightarrow x^-_0}f(x)≠\lim\limits_{x\rightarrow x^+_0}f(x)\end{cases}

第二类{无穷型间断点：lim⁡x→x0−f(x)=∞或lim⁡x→x0+f(x)=∞.震荡型间断点：lim⁡x→x0f(x)震荡.第二类\begin{cases} 无穷型间断点：\\\qquad\lim\limits_{x\rightarrow x^-_0}f(x)=\infty或\lim\limits_{x\rightarrow x^+_0}f(x)=\infty.\\震荡型间断点：\\\qquad\lim\limits_{x\rightarrow x_0}f(x)震荡.\end{cases}

微分的几何意义

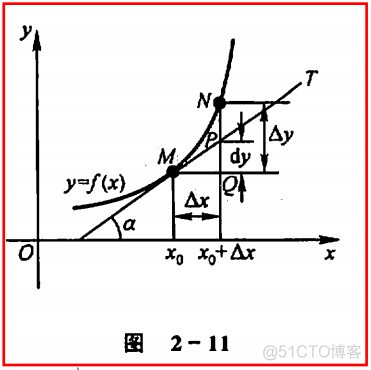
image-1659454995781

导数表

image-1659455083825
莱布尼兹公式
(uv)(n)=∑k=0nCnku(n−k)v(k)(uv)^{(n)}=\sum\limits^n_{k=0}C^k_nu^{(n-k)}v^{(k)}

中值定理

image-1659929982471
image-1659929991507
image-1659929999887
image-1659930011291
image-1659930019852
image-1659930028738
image-1659930038597
image-1659930047124
image-1659930055543
image-1659930063883

数列极限转积分

∫01f(x)dx=∑k=1n1nf(kn)\int_{0}^{1}f(x)dx=\sum\limits_{k=1}^n\frac{1}{n}f(\frac{k}{n})

基本积分公式

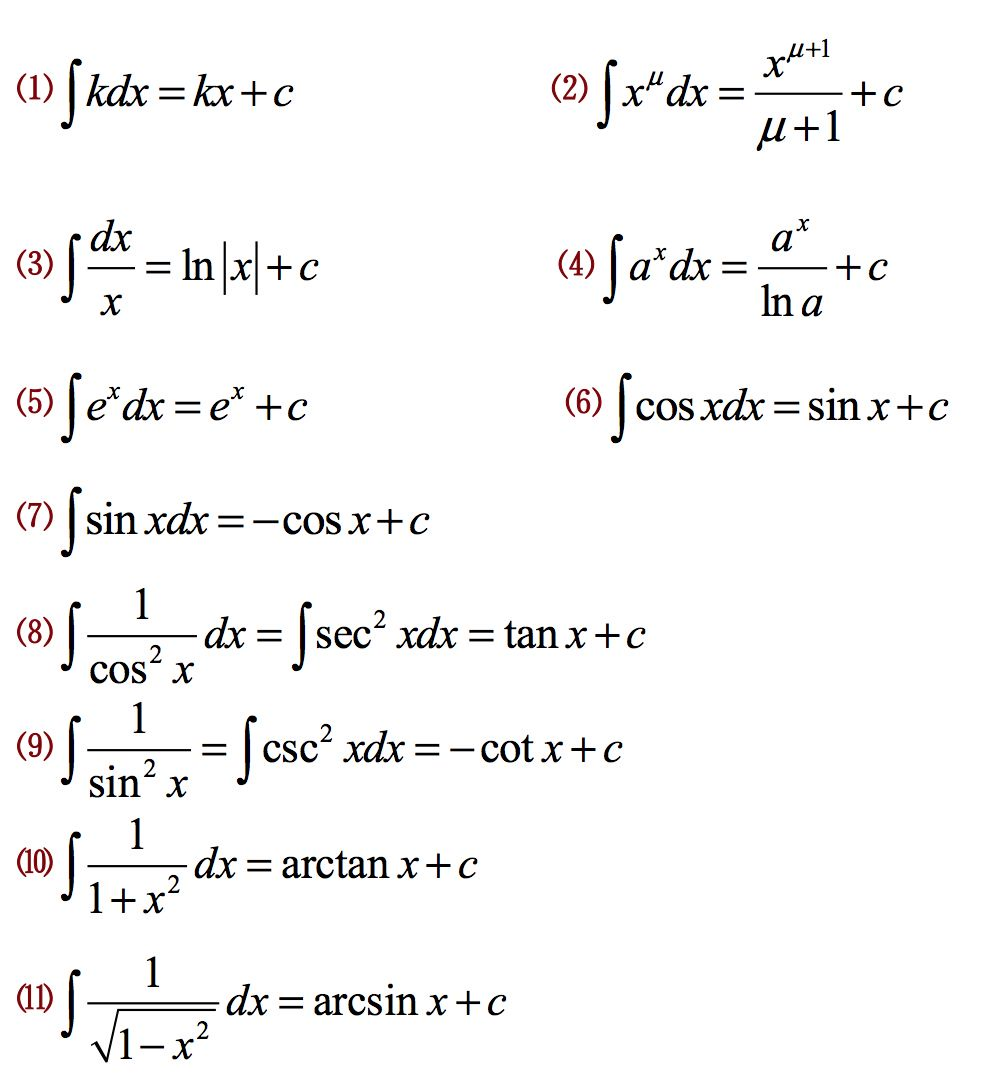
image-1659930220159
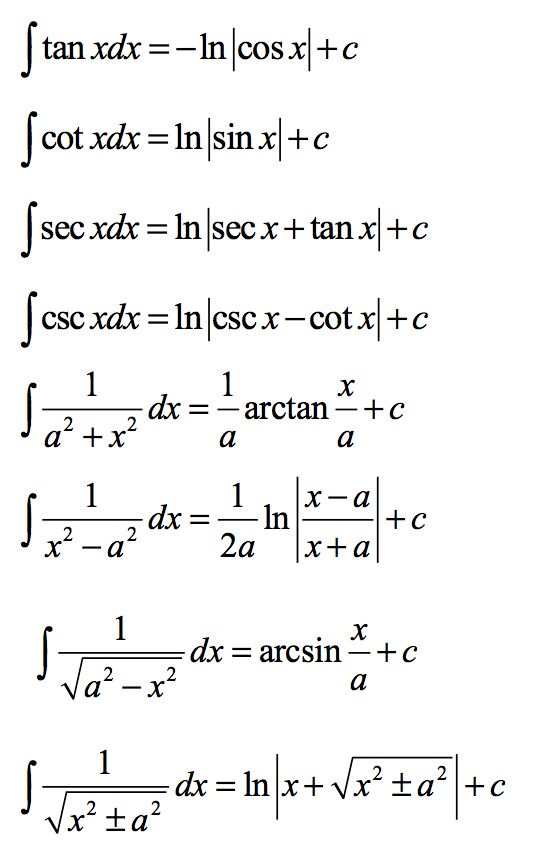
image-1659930237030

常见的换元法

以下式子中，R(u,v)R(u,v) 表示 uu，vv 的有理函数.

  1. ∫R(x,a2−x2)dx\int R(x,\sqrt{a^2-x^2})dx，∫R(x,x2±a2)dx\int R(x,\sqrt{x^2±a^2})dx 型，a>0a>0.可以通过画一个直角三角形来快速判断x应当如何换元
    • 含 a2−x2\sqrt{a^2-x^2}，令 x=asin⁡tx=a\sin t，dx=acos⁡tdtdx=a\cos t dt，
    • 含 x2+a2\sqrt{x^2+a^2}，令 x=atan⁡tx=a\tan t，dx=asec⁡2tdtdx=a\sec^2 t dt，
    • 含 x2−a2\sqrt{x^2-a^2}，令 x=asec⁡tx=a\sec t，dx=asec⁡ttan⁡tdtdx=a\sec t\tan t dt.
  2. ∫R(x,ax+bn,ax+bm)dx\int R(x,\sqrt[n]{ax+b},\sqrt[m]{ax+b})dx 型，a≠0a≠0.
    • 令 ax+bmn=t\sqrt[mn]{ax+b}=t，x=tmn−bax=\frac{t^{mn}-b}{a}，dx=mnatmn−1dtdx=\frac{mn}{a}t^{mn-1}dt.
  3. ∫R(x,ax+bcx+d)dx\int R(x,\sqrt{\frac{ax+b}{cx+d}})dx 型
    • 令 ax+bcx+d=t\sqrt{\frac{ax+b}{cx+d}}=t，x=dt2−ba−ct2x=\frac{dt^2-b}{a-ct^2}，dx=2(ad−bc)t(a−ct2)2dtdx=\frac{2(ad-bc)t}{(a-ct^2)^2}dt.其中设 ad−bc≠0ad-bc≠0.
  4. 万能代换∫R(sin⁡x,cos⁡x)\int R(\sin x,\cos x)型：
    • 令 tan⁡x2=t\tan \frac{x}{2}=t，则 sin⁡x=2t1+t2\sin x=\frac{2t}{1+t^2}，cos⁡x=1−t21+t2\cos x=\frac{1-t^2}{1+t^2}，dx=21+t2dtdx=\frac{2}{1+t^2}dt.

分部积分法

设 u(x)u(x)，v(x)v(x) 均有连续导数，则

∫u(x)v′(x)dx=u(x)v(x)−∫v(x)u′(x)dx\int u(x)v'(x)dx=u(x)v(x)-\int v(x)u'(x)dx

或

∫u(x)dv(x)=u(x)v(x)−∫v(x)du(x)\int u(x)dv(x)=u(x)v(x)-\int v(x)du(x)

以及

∫abu(x)v′(x)dx=u(x)v(x)∣ab−∫abv(x)u′(x)dx\int^b_a u(x)v'(x)dx=u(x)v(x)\Big|^b_a-\int^b_a v(x)u'(x)dx

或

∫abu(x)dv(x)=u(x)v(x)∣ab−∫abv(x)du(x)\int^b_a u(x)dv(x)=u(x)v(x)\Big|^b_a-\int^b_a v(x)du(x)

参考链接

https://blog.csdn.net/nantongcjq/article/details/78987467