CUDA编程实现求解单源Bellman-Ford最短路径算法
CUDA介绍
什么类型的程序适合在GPU上运行?
- 计算密集型的程序。
- 易于并行的程序。GPU其实是一种SIMD(Single Instruction Multiple Data)架构。
CUDA是什么?
- CUDA,全称是Compute Unified Device Architecture,英伟达在2007年推出这个统一计算架构,为了让GPU有可用的编程环境,从而能通过程序控制底层的硬件进行计算。
- CUDA提供host-device的编程模式以及非常多的接口函数和科学计算库,通过同时执行大量的线程而达到并行的目的。CUDA也有不同的版本,从1.0开始到现在的8.0,每个版本都会有一些新特性。CUDA是基于C语言的扩展,例如扩展了一些限定符device、shared等,从3.0开始也支持
C++编程,从7.0开始支持C++11。
算法流程
- 初始化
- 通过读文件的形式将数据读入到一维数组中
- 松弛(重点部分)
- 该部分是本算法中计算量最大的部分,也是使用GPU进行计算的部分
- 通过给一维数组中的顶点分配线程并行进行松弛操作,来有效降低运行时间
- 检验是否有负权环
- 结果输出
- 将结果输出到
output.txt中,若不存在负权环,则输出最小距离;若存在负权环,则输出FOUND NEGATIVE CYCLE!
- 将结果输出到
算法代码
输入格式
- 第一行是一个整数
N,表示输入图中的顶点数; - 下面的N行是一个
N*N邻接矩阵; - 记行为
v,列为w,那么mat[v][w]是指从顶点v到顶点w的距离(权重); - 所有的距离都是整数;
- 如果没有边连接顶点
v和w,那么mat[v][w]将使用1000000(INF)来表示无穷大; - 顶点的序号是非负连续的整数,对于一个有
N个顶点的输入图,顶点将被标记为0,1,2,… ,N-1; - 我们总是使用顶点0作为源顶点。
输出格式
- 输出文件包含从
顶点0到所有顶点的距离,按照顶点序号(0,1,2,… )的递增顺序,每行一个距离; - 如果至少有一个负循环(图中循环的权重之和为负) ,程序将变量
has_NEGATIVE_CYCLE设置为 true 并打印"FOUND NEGATIVE CYCLE!"(发现负权环),因为此时没有最短路径。
核函数结构
// GPU执行 CPU调用
bellman_ford_one_iter<<<blocks, threads>>>(n, d_mat, d_dist, d_has_next, iter_num);
// 核函数
// __global__ GPU执行部分 核函数
// n:顶点数量
// d_mat:矩阵
// d_dist:距离
// blockDim.x是线程块在x方向上的线程数(在x方向上每一个线程块有多少个线程)
// blockIdx.x是线程块在x方向上的索引
// threadIdx.x是线程在X方向上的索引(在自己的线程块内)
// gridDim.x表示x方向有几个block
__global__ void bellman_ford_one_iter(int n, int *d_mat, int *d_dist, bool *d_has_next, int iter_num) {
int global_tid = blockDim.x * blockIdx.x + threadIdx.x; // 计算线程号global_tid 一维只需要在x方向上做计算
int elementSkip = blockDim.x * gridDim.x;
if(global_tid >= n) return;
for(int u = 0 ; u < n ; u ++) {
for(int v = global_tid; v < n; v+= elementSkip) {
int weight = d_mat[u * n + v];
if(weight < INF) {
// 松弛操作
int new_dist = d_dist[u] + weight;
if(new_dist < d_dist[v]) {
d_dist[v] = new_dist;
*d_has_next = true;
}
}
}
}
}
核函数线程分配
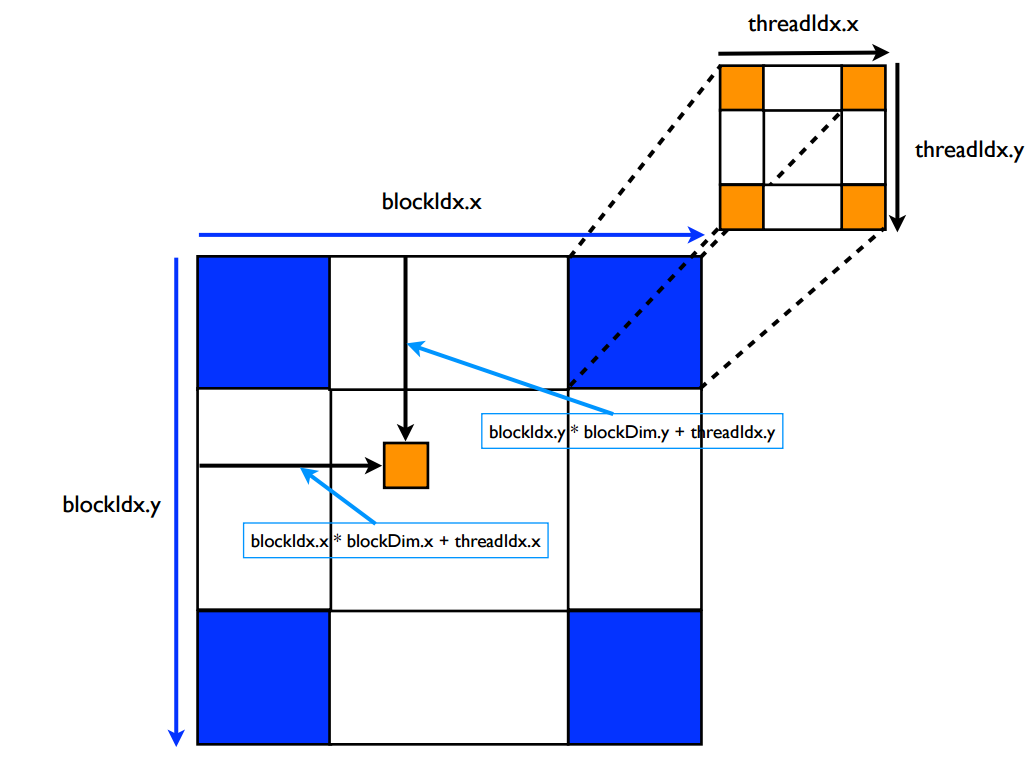
优化策略
通过利用GPU进行并行编程,提高了算法效率,尤其在数据集较大的情况下更为明显。
源代码
// 这是CUDA版本的单源Bellman-Ford最短路径算法
// 编译
// nvcc cuda.cu -o cuda
// 运行
// ./cuda input1.txt <每个网格的线程块的数量> <每个线程块的线程数量>
// 可以在output.txt中看到结果记录
#include <string>
#include <cassert>
#include <iostream>
#include <fstream>
#include <algorithm>
#include <iomanip>
#include <cstring>
#include <sys/time.h>
#include <cuda_runtime.h>
#include <device_launch_parameters.h>
// using namespace std 的进化版本
using std::string;
using std::cout;
using std::endl;
// 无穷大
#define INF 1000000
/*
* This is a CHECK function to check CUDA calls
*/
#define CHECK(call) { \
const cudaError_t error = call; \
if (error != cudaSuccess) { \
fprintf(stderr, "Error: %s:%d, ", __FILE__, __LINE__); \
fprintf(stderr, "code: %d, reason: %s\n", error, cudaGetErrorString(error)); \
exit(1); \
} \
}
// utils是实用程序功能的命名空间
// 包括I/O(读取输入文件和打印结果)和矩阵维度转换(2D->1D)函数
namespace utils {
int N; // 顶点数量
int *mat; // the adjacency matrix 邻接矩阵
void abort_with_error_message(string msg) {
std::cerr << msg << endl;
abort();
}
// 将二维转换为一维
int convert_dimension_2D_1D(int x, int y, int n) {
return x * n + y;
}
// 读取文件 获取整个矩阵 并经过转换存储在一维数组中
int read_file(string filename) {
std::ifstream inputf(filename, std::ifstream::in);
if (!inputf.good()) {
abort_with_error_message("ERROR OCCURRED WHILE READING INPUT FILE");
}
inputf >> N;
// 对输入的矩阵做一个 20MB * 20MB 的限制 (400MB)
assert(N < (1024 * 1024 * 20));
mat = (int *) malloc(N * N * sizeof(int));
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++) {
// 通过convert_dimension_2D_1D函数将二维数据转换成一维存放到mat数组中
inputf >> mat[convert_dimension_2D_1D(i, j, N)];
}
return 0;
}
// 结果输出到output.txt中
int print_result(bool has_negative_cycle, int *dist) {
std::ofstream outputf("output.txt", std::ofstream::out);
if (!has_negative_cycle) { // 不含有负权环则输出正确结果到文件中
for (int i = 0; i < N; i++) {
if (dist[i] > INF)
dist[i] = INF;
outputf << dist[i] << '\n';
}
outputf.flush();
} else { // 含有负权环 输出FOUND NEGATIVE CYCLE!
outputf << "FOUND NEGATIVE CYCLE!" << endl;
}
outputf.close();
return 0;
}
} // utils命名空间
// __global__ GPU执行部分 核函数
// n:顶点数量
// d_mat:矩阵
// d_dist:距离
// blockDim.x是线程块在x方向上的线程数(在x方向上每一个线程块有多少个线程)
// blockIdx.x是线程块在x方向上的索引
// threadIdx.x是线程在X方向上的索引(在自己的线程块内)
// gridDim.x表示x方向有几个block
__global__ void bellman_ford_one_iter(int n, int *d_mat, int *d_dist, bool *d_has_next, int iter_num) {
int global_tid = blockDim.x * blockIdx.x + threadIdx.x; // 计算线程号global_tid 一维只需要在x方向上做计算
int elementSkip = blockDim.x * gridDim.x;
if(global_tid >= n) return;
for(int u = 0 ; u < n ; u ++) {
for(int v = global_tid; v < n; v+= elementSkip) {
int weight = d_mat[u * n + v];
if(weight < INF) {
// 松弛操作
int new_dist = d_dist[u] + weight;
if(new_dist < d_dist[v]) {
d_dist[v] = new_dist;
*d_has_next = true;
}
}
}
}
}
// Bellman-Ford算法。找到从顶点0到其他顶点的最短路径。
/**
* @param blockPerGrid 每个网格中线程块的个数
* @param threadsPerBlock 每个线程块中线程的个数
* @param n input size
* @param *mat input adjacency matrix
* @param *dist 距离数组
* @param *has_negative_cycle 一个记录是否含有负权环的变量
*/
void bellman_ford(int blocksPerGrid, int threadsPerBlock, int n, int *mat, int *dist, bool *has_negative_cycle) {
dim3 blocks(blocksPerGrid);
dim3 threads(threadsPerBlock);
// 计数 记录循环次数
int iter_num = 0;
int *d_mat, *d_dist;
bool *d_has_next, h_has_next;
// GPU全局内存分配
// cudaError_t cudaMalloc(void **devPtr, size_t size);
cudaMalloc(&d_mat, sizeof(int) * n * n);
cudaMalloc(&d_dist, sizeof(int) *n);
cudaMalloc(&d_has_next, sizeof(bool));
// 是否有负权环的标志位
*has_negative_cycle = false;
// 初始化 将所有距离置为无穷大
for(int i = 0 ; i < n; i ++) {
dist[i] = INF;
}
// 到自己的距离置为0
dist[0] = 0;
// CPU与GPU内存同步拷贝
// cudaError_t cudaMemcpy(void *dst, const void *src, size_t count, cudaMemcpyKind kind)
// kind: cudaMemcpyHostToHost, cudaMemcpyHostToDevice, cudaMemcpyDeviceToHost, cudaMemcpyDeviceToDevice, or cudaMemcpyDefault
cudaMemcpy(d_mat, mat, sizeof(int) * n * n, cudaMemcpyHostToDevice);
cudaMemcpy(d_dist, dist, sizeof(int) * n, cudaMemcpyHostToDevice);
for(;;) {
h_has_next = false;
cudaMemcpy(d_has_next, &h_has_next, sizeof(bool), cudaMemcpyHostToDevice);
// 松弛操作 由GPU进行
bellman_ford_one_iter<<<blocks, threads>>>(n, d_mat, d_dist, d_has_next, iter_num);
CHECK(cudaDeviceSynchronize());
cudaMemcpy(&h_has_next, d_has_next, sizeof(bool), cudaMemcpyDeviceToHost);
iter_num++; // 循环次数加一
if(iter_num >= n-1) { // 如果循环次数大于n-1 说明存在负权环
*has_negative_cycle = true;
break;
}
if(!h_has_next) {
break;
}
}
if(! *has_negative_cycle) {
cudaMemcpy(dist, d_dist, sizeof(int) * n, cudaMemcpyDeviceToHost);
}
// GPU全局内存释放
// cudaError_t cudaFree(void *devPtr);
cudaFree(d_mat);
cudaFree(d_dist);
cudaFree(d_has_next);
}
int main(int argc, char **argv) {
if (argc <= 1) { // 没有写输入文件的情况
utils::abort_with_error_message("INPUT FILE WAS NOT FOUND!");
}
if (argc <= 3) { // 没有写块数量或者进程数的情况
utils::abort_with_error_message("blocksPerGrid or threadsPerBlock WAS NOT FOUND!");
}
// 保存输入文件名
string filename = argv[1];
// 每个网格中线程块的个数
int blockPerGrid = atoi(argv[2]);
// 每个线程块中线程的个数
int threadsPerBlock = atoi(argv[3]);
int *dist;
bool has_negative_cycle = false;
assert(utils::read_file(filename) == 0);
dist = (int *) calloc(sizeof(int), utils::N);
// 计时器
timeval start_wall_time_t, end_wall_time_t;
float ms_wall;
cudaDeviceReset();
// 开始计时
gettimeofday(&start_wall_time_t, nullptr);
//bellman-ford算法
bellman_ford(blockPerGrid, threadsPerBlock, utils::N, utils::mat, dist, &has_negative_cycle);
CHECK(cudaDeviceSynchronize());
// 结束计时
gettimeofday(&end_wall_time_t, nullptr);
ms_wall = ((end_wall_time_t.tv_sec - start_wall_time_t.tv_sec) * 1000 * 1000
+ end_wall_time_t.tv_usec - start_wall_time_t.tv_usec) / 1000.0;
std::cerr.setf(std::ios::fixed);
std::cerr << std::setprecision(6) << "Time(s): " << (ms_wall/1000.0) << endl;
utils::print_result(has_negative_cycle, dist);
free(dist);
free(utils::mat);
return 0;
}
测试结果
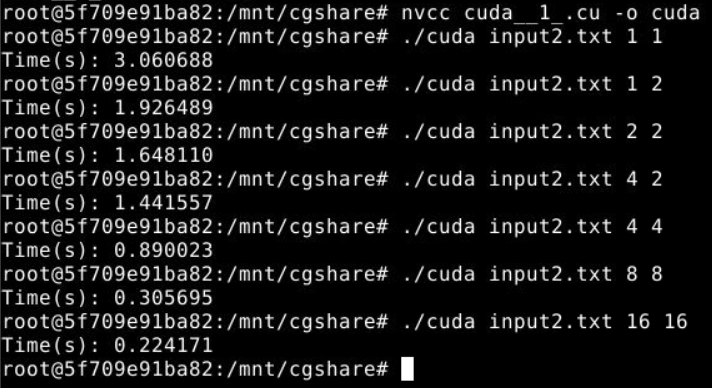
测试结果分析
- 在数据集方面,我们有一个
4*4的矩阵输入和一个1500*1500的矩阵输入作为对照,分别测试运行时间以及提速效果,显然数据集越大,CUDA的效果越明显; - 通过对
4*4矩阵输入的结果输出output.txt文件进行分析,确定计算结果无误; - 在代码运行方面,以
1500*1500的矩阵作为固定输入,显然,随着blockPerGrid和threadsPerBlock的增加,运行时间越来越短,这是实验中我们最期望看到的理想状况。
不足和改进之处
- 由于本次实验数据集我们只找到了
1500*1500的,数据规模虽然可以体现出改进的效果,但是还有更大的进步空间; - 为了方便起见,我们使用的是一维进行操作,可以经过进一步改进,改成高维计算。