浅谈单源Bellman-Ford最短路径算法
算法说明
- Bellman-Ford 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-Source Shortest Path)的算法。
- 对于带权有向图 G = (V, E),Dijkstra 算法要求图 G 中边的权值均为非负,而Bellman-ford能适应一般的情况(即存在负权边的情况)。
- Bellman-ford 采用动态规划的方法,实现的时间复杂度为 O(V*E),其中 V 为顶点数量,E 为边的数量。
- Dijkstra 算法采用贪心算法的方法,普通实现的时间复杂度为 O(V^2)。若使用优先队列则时间复杂度为 O(E + VlogV)。
Bellman-Ford 算法描述
- 创建源顶点 v 到图中所有顶点的距离的集合 distSet,为图中的所有顶点指定一个距离值,初始均为 Infinite,源顶点距离为 0;
- 计算最短路径,执行 V - 1 次遍历;
- 对于图中的每条边:如果起点 u 的距离 d 加上边的权值 w 小于终点 v 的距离 d,则更新终点 v 的距离值 d;(即松弛操作)
- 检测图中是否有负权边形成了环,遍历图中的所有边,计算 u 至 v 的距离,如果对于 v 存在更小的距离,则说明存在环;
伪代码
字母定义
G:图
w:权重二维数组,反映的是u到v的边的权重。
s:起点
for循环解释
第一个双重for循环:循环V - 1次,对于每个边,都进行松弛操作;
第二个for循环:检查是否有环。
- 因为已经进行了V-1次循环了,理论上不应该可以松弛;
- 但如果还有可以松弛的,说明存在负权环,返回False,否则返回true。
为什么要循环V-1次?
因为最短路径肯定是个简单路径,不可能包含回路,如果包含回路,但回路的权值和为正,也松弛不了,还是可以得到更短的路径。但如果回路的权值是负的,就可以一直松弛,那么肯定没有解。图有n个点,又不能有回路,所以最短路径最多n-1边(可以想象成一条线)。又因为每次循环至少松弛一条边,所以最多n-1次就行了。
Bellman-ford
// BELLMAN-FORD(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
// 初始化
for all u ∈ V
d[u] = ∞
π[u] = nil
d[s] = 0
// 松弛操作
for i = 1 to |V[G]| - 1
for each edge (u, v) ∈ E[G]
RELAX(u, v, w)
// 检查是否存在负权环
for each edge (u, v) ∈ E[G]
if d[v] > d[u] + w(u, v)
then return FALSE
return TRUE
松弛操作
// 对u节点到v节点的距离进行的松弛操作,如果到u的距离加上u到v的边小于到v的距离,那么可以缩短距离,更新之。
// RELAX(u, v, w)
if d[v] > d[u] + w(u, v)
d[v] = d[u] + w(u, v)
π[v] = u // 前置数组 原本被初始化为空 用于存储当前路径的上一个点是什么
例子
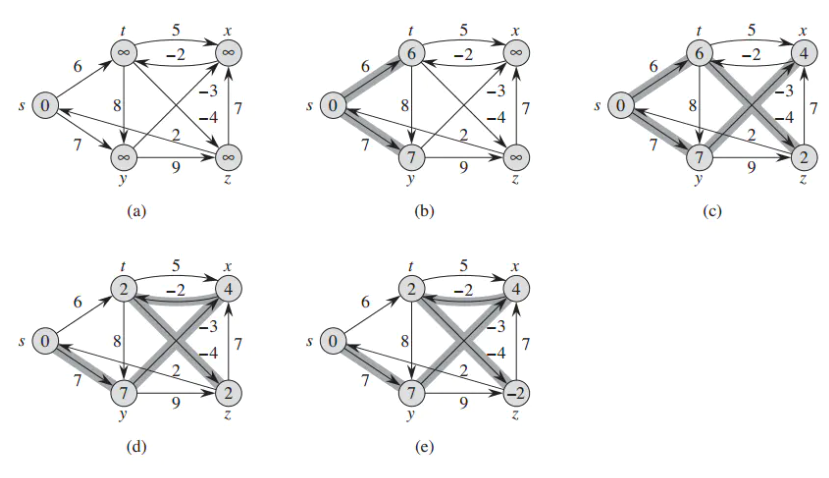
- 初始化:源节点到自己的距离为0,到其他节点的距离为∞;
- 对于源节点的
邻接节点,比较从源节点加上边的和与其本身距离的值,若小,则更新。以此类推,循环 V - 1 次(即节点数减1次)。 - 最后检查是否还可以松弛,如果可以,说明有环,返回false。