AcWing 785. 快速排序

题目

给定你一个长度为 $n$ 的整数数列。

请你使用快速排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 $n$。

第二行包含 $n$ 个整数（所有整数均在 $1∼10^9$ 范围内），表示整个数列。

输出格式
输出共一行，包含 $n$ 个整数，表示排好序的数列。

数据范围
$1≤n≤100000$

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

思路

基于数组存储

直接插入排序

复杂度

1. 时间复杂度
   • 最好情况：$O(n)$
   • 平均情况：$O(n^2)$
   • 最坏情况：$O(n^2)$
2. 辅助空间复杂度：$O(1)$
3. 稳定

图示

代码

void insert_sort()  // 直接插入排序
{
    for (int i = 1; i < n; i ++ )
    {
        int t = q[i], j = i;
        while (j && q[j - 1] > t)
        {
            q[j] = q[j - 1];
            j -- ;
        }
        q[j] = t;
    }
}

折半插入排序

是直接插入排序的一个优化版，插入时由依次遍历寻找改为折半查找，仅仅是移动次数发生了改变，不影响最终的复杂度。

复杂度

1. 时间复杂度
   • 最好情况：$O(n)$
   • 平均情况：$O(n^2)$
   • 最坏情况：$O(n^2)$
2. 辅助空间复杂度：$O(1)$
3. 稳定

代码

void binary_search_insert_sort()  // 折半插入排序
{
    for (int i = 1; i < n; i ++ )
    {
        if (q[i - 1] <= q[i]) continue;
        int t = q[i];
        int l = 0, r = i - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (q[mid] > t) r = mid;
            else l = mid + 1;
        }
        for (int j = i - 1; j >= r; j -- )
            q[j + 1] = q[j];
        q[r] = t;
    }
}

冒泡排序

复杂度

1. 时间复杂度
   • 最好情况：$O(n)$
   • 平均情况：$O(n^2)$
   • 最坏情况：$O(n^2)$
2. 辅助空间复杂度：$O(1)$
3. 稳定

图示

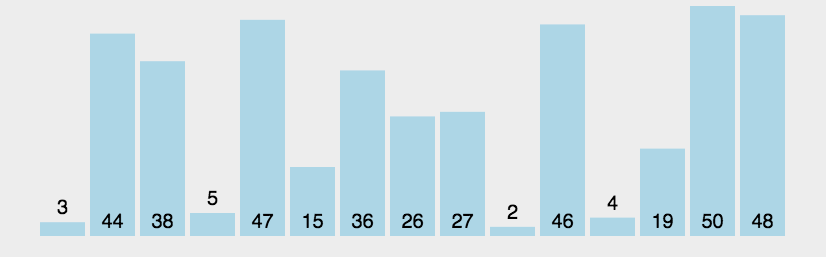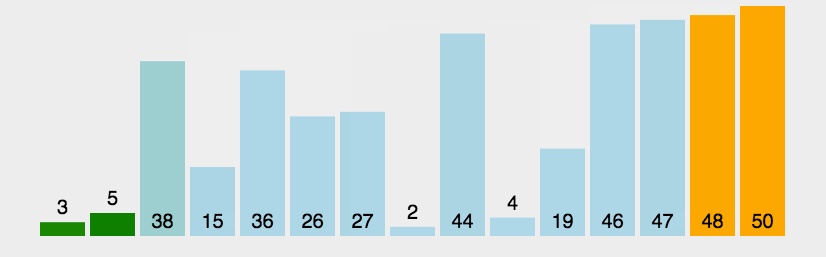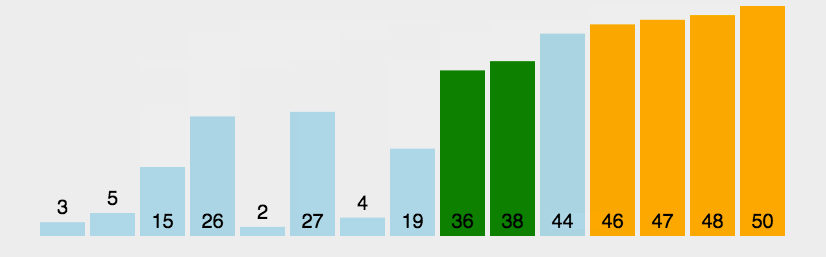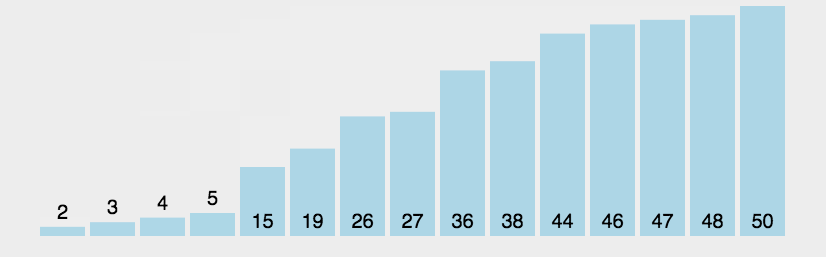
优化
当我们发现每一对相邻元素都不需要互换的时候，说明已经有序，可以提前退出。

代码

void bubble_sort()  // 冒泡排序
{
    for (int i = 0; i < n - 1; i ++ )
    {
        bool has_swap = false;
        for (int j = n - 1; j > i; j -- )
            if (q[j] < q[j - 1])
            {
                swap(q[j], q[j - 1]);
                has_swap = true;
            }
        if (!has_swap) break;
    }
}

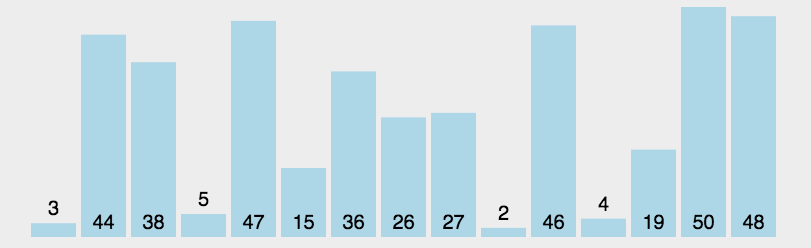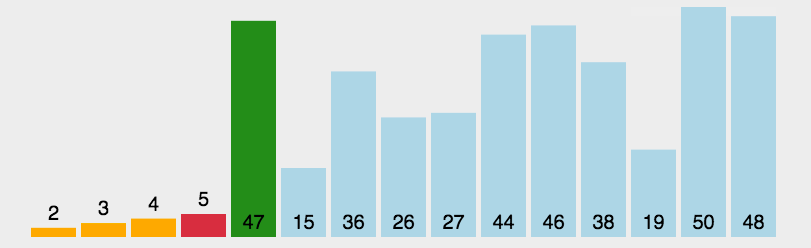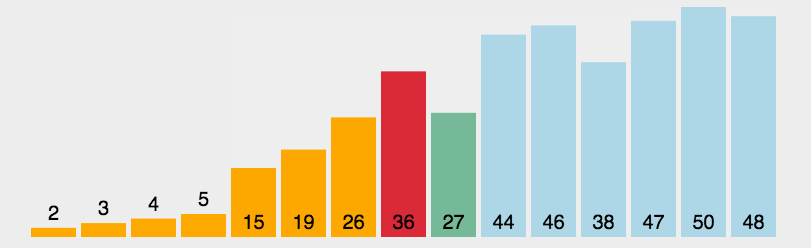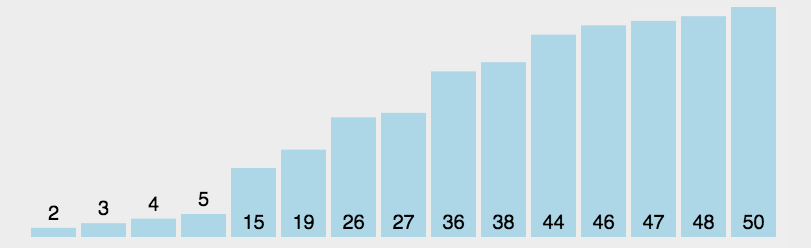
简单选择排序

复杂度

1. 时间复杂度
   • 最好情况：$O(n^2)$
   • 平均情况：$O(n^2)$
   • 最坏情况：$O(n^2)$
2. 辅助空间复杂度：$O(1)$
3. 不稳定

图示

代码

void select_sort()  // 简单选择排序
{
    for (int i = 0; i < n - 1; i ++ )
    {
        int k = i;
        for (int j = i + 1; j < n; j ++ )
            if (q[j] < q[k])
                k = j;
        swap(q[i], q[k]);
    }
}

希尔排序

每组内的下标是等差数列
组内使用插入排序(因为插入排序对于部分有序的序列效率很高)
复杂度

1. 时间复杂度 $O(n^{\frac{3}{2}})$
2. 辅助空间复杂度：$O(1)$
3. 不稳定

图示动图是分组执行，实际操作是多个分组交替执行

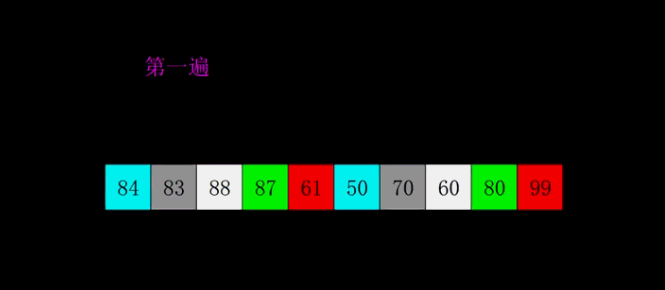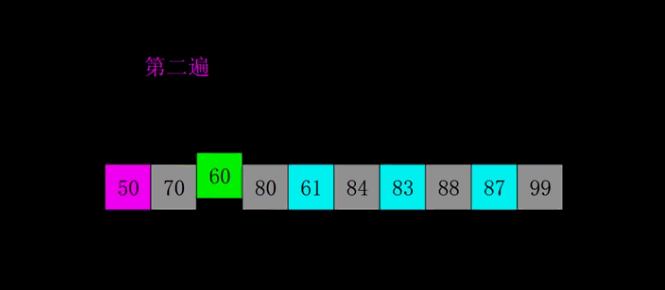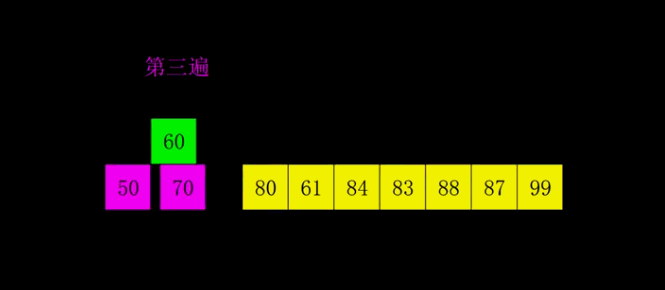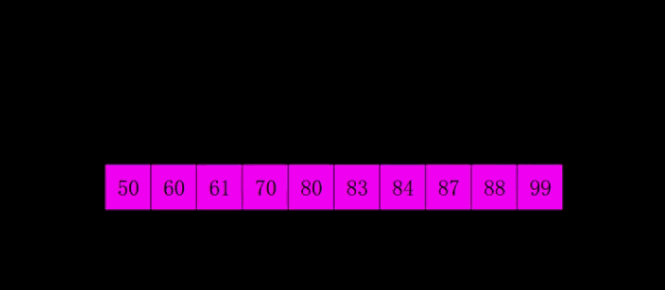
代码

void shell_sort()  // 希尔排序
{
    for (int d = n / 3; d; d = d == 2 ? 1 : d / 3)
    {
        for (int start = 0; start < d; start ++ )
        {
            for (int i = start + d; i < n; i += d)
            {
                int t = q[i], j = i;
                while (j > start && q[j - d] > t)
                {
                    q[j] = q[j - d];
                    j -= d;
                }
                q[j] = t;
            }
        }
    }
}

快速排序

最好背一个
步骤

1. 找分界点
2. 划分成2段
3. 递归排左右两边

复杂度

1. 时间复杂度
   • 最好情况：$O(n\log n)$
   • 平均情况：$O(n\log n)$
   • 最坏情况：$O(n^2)$
2. 辅助空间复杂度：$O(\log n)$
3. 不稳定

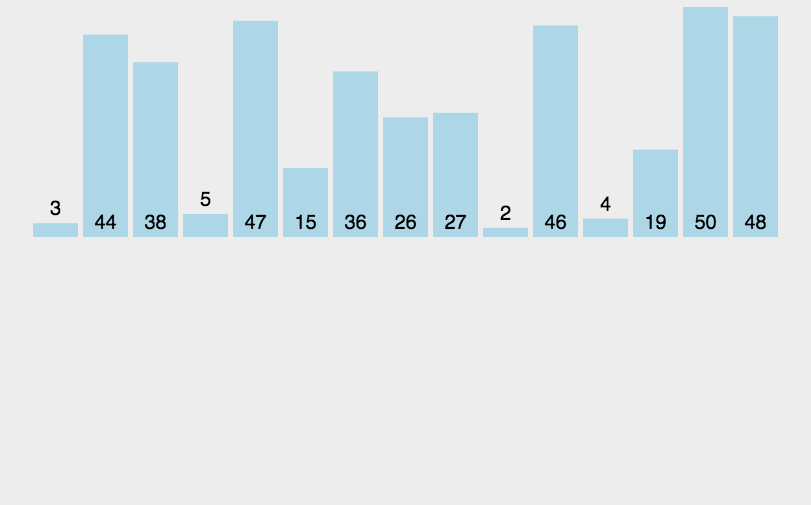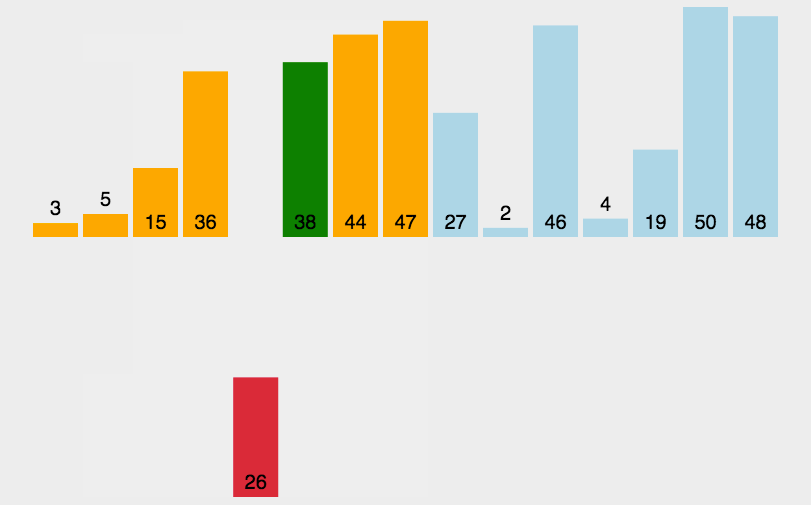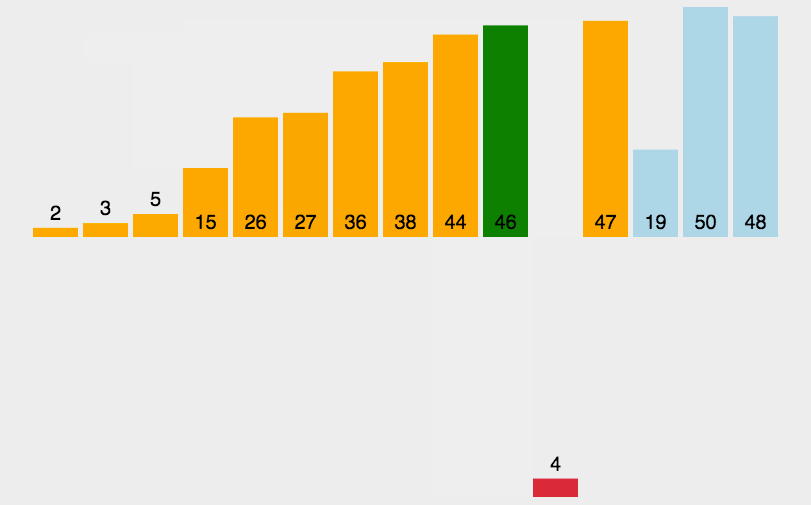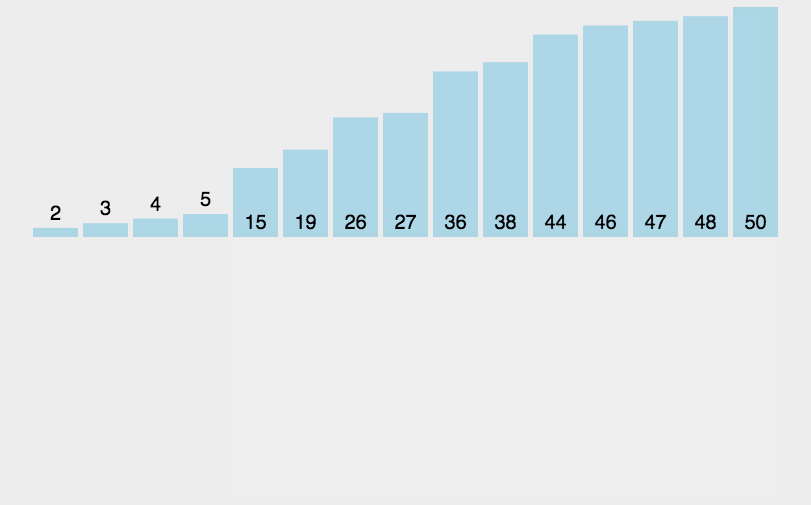
图示

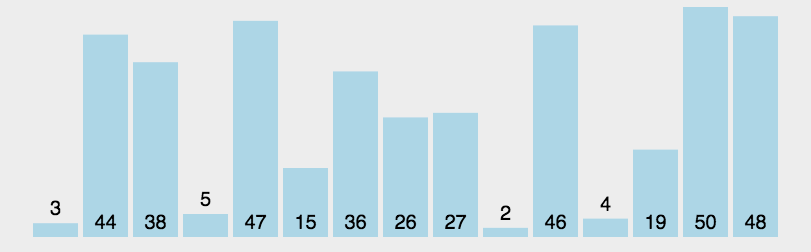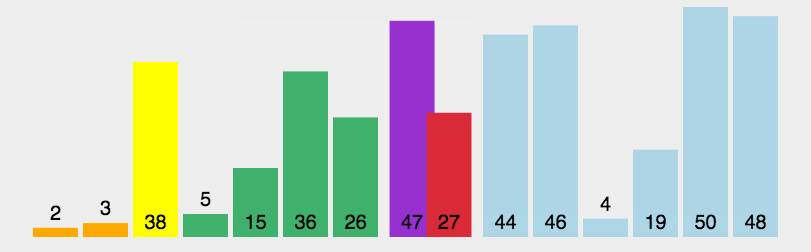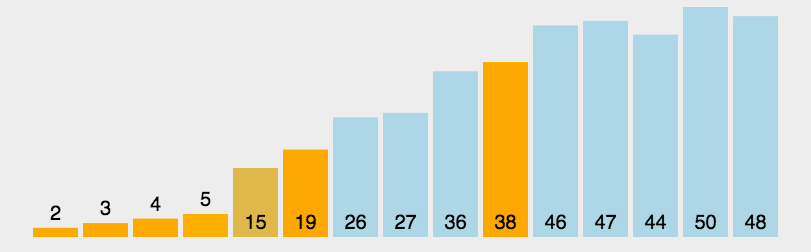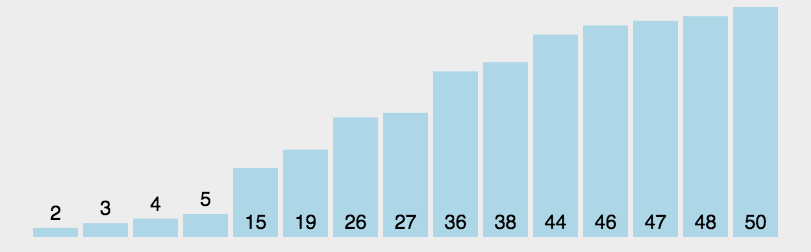
代码

void quick_sort(int l, int r)  // 快速排序
{
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[(l + r) / 2];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(l, j);
    quick_sort(j + 1, r);
}

堆排序

以大根堆为例
对于每一个结点来说，都有根结点≥子结点，所以有根节点是整个树的最大值。
堆一般使用顺序存储，根节点编号为x，则左儿子为2x，右儿子为2x+1
堆的建立：从下往上递归创建
堆的删除(删除堆顶)：将最后一个元素放到堆顶，然后进行down操作即可

复杂度

1. 时间复杂度
   • 最好情况：$O(n\log n)$
   • 平均情况：$O(n\log n)$
   • 最坏情况：$O(n\log n)$
2. 辅助空间复杂度：$O(\log n)$
3. 不稳定

图示

代码

void down(int u)
{
    int t = u;
    if (u * 2 <= sz && q[u * 2] > q[t]) t = u * 2;
    if (u * 2 + 1 <= sz && q[u * 2 + 1] > q[t]) t = u * 2 + 1;

    if (u != t)
    {
        swap(q[u], q[t]);
        down(t);
    }
}![heapSort](/upload/2022/08/heapSort.gif)

void heap_sort()  // 堆排序，下标一定要从1开始
{
    sz = n;
    for (int i = n / 2; i; i -- ) down(i);

    for (int i = 0; i < n - 1; i ++ )
    {
        swap(q[1], q[sz]);
        sz -- ;
        down(1);
    }
}

归并排序

1. 递归 [L,mid] [mid+1,R]
2. 二路归并
   • 先排成两个有序数组
   • 然后将两个有序数组合并成一个有序数组

复杂度

1. 时间复杂度
   • 最好情况：$O(n\log n)$
   • 平均情况：$O(n\log n)$
   • 最坏情况：$O(n\log n)$
2. 辅助空间复杂度：$O(n)$
3. 稳定

图示

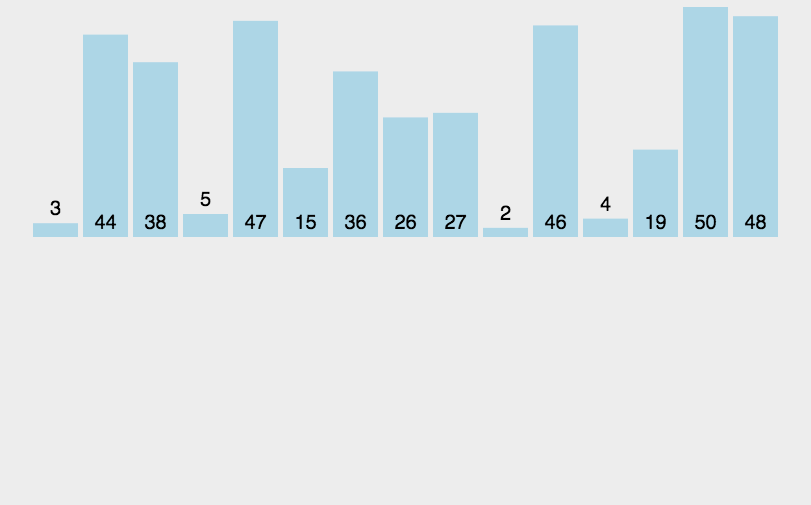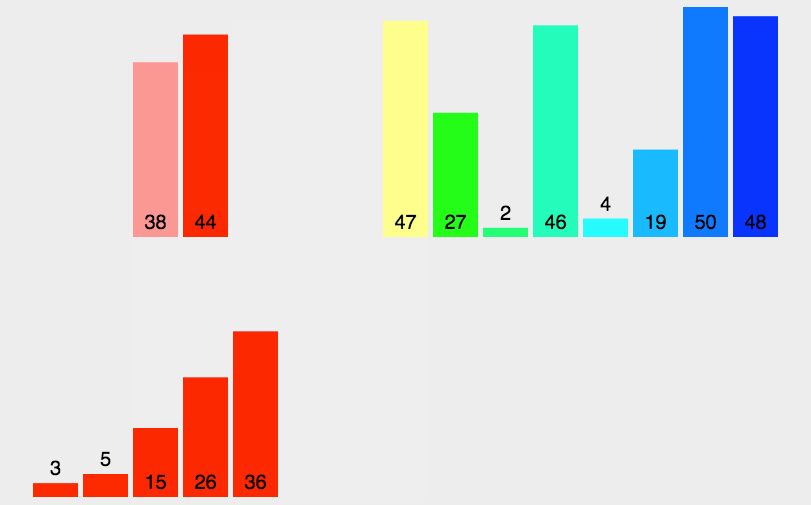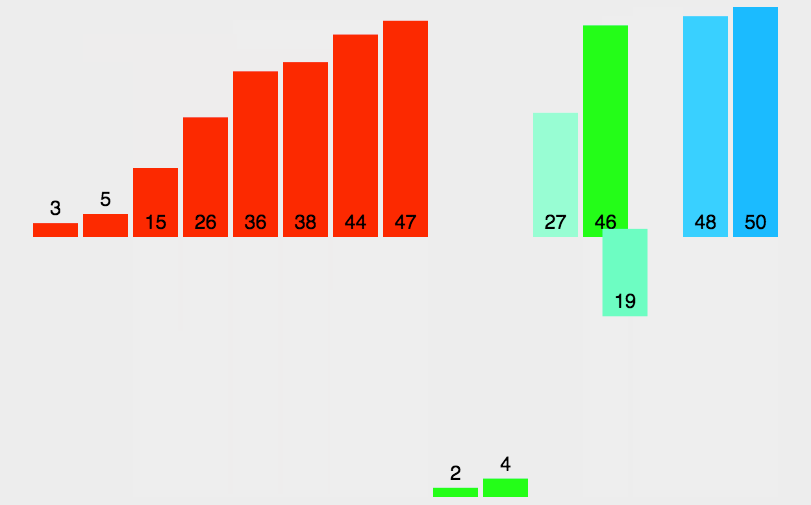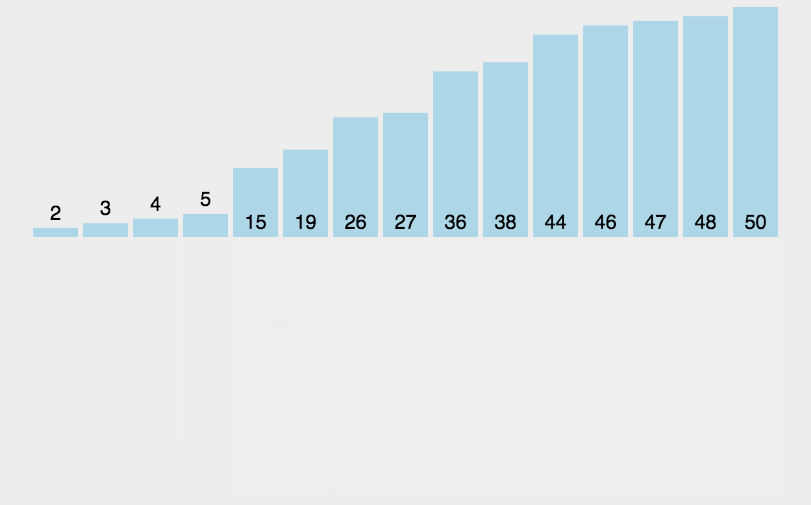
代码

void merge_sort(int l, int r)
{
    if (l >= r) return;
    int mid = l + r >> 1;
    merge_sort(l, mid), merge_sort(mid + 1, r);
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) w[k ++ ] = q[i ++ ];
        else w[k ++ ] = q[j ++ ];
    while (i <= mid) w[k ++ ] = q[i ++ ];
    while (j <= r) w[k ++ ] = q[j ++ ];
    for (i = l, j = 0; j < k; i ++, j ++ ) q[i] = w[j];
}

桶排序(计数排序)

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。
桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

• 步骤：
  • 设置一个定量的数组当作空桶；
  • 遍历输入数据，并且把数据一个一个放到对应的桶里去；
  • 对每个不是空的桶进行排序；
  • 从不是空的桶里把排好序的数据拼接起来。

复杂度

1. 时间复杂度
   • 最好情况：$O(n+m)$
   • 平均情况：$O(n+m)$
   • 最坏情况：$O(n+m)$
2. 辅助空间复杂度：$O(n+m)$
3. 稳定

图示
计数排序

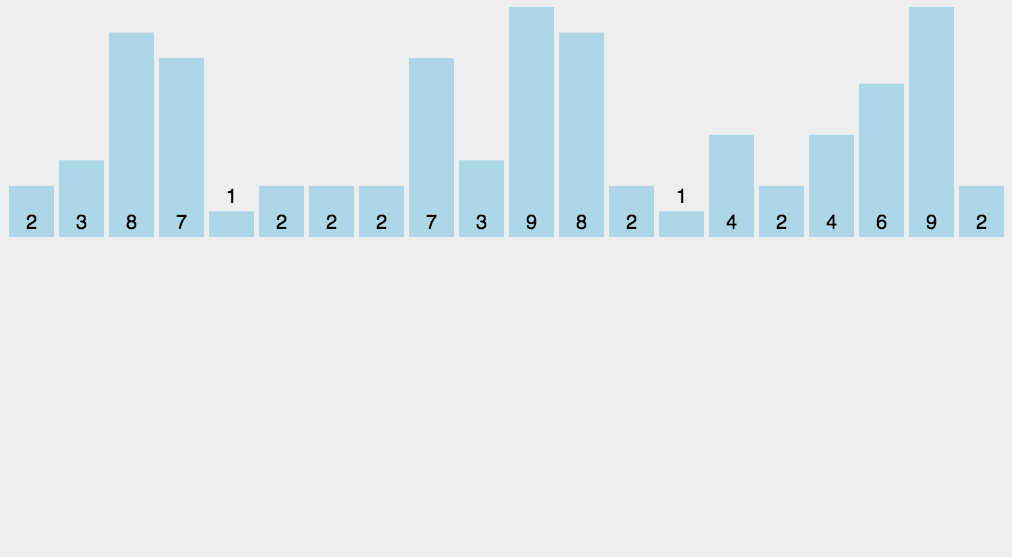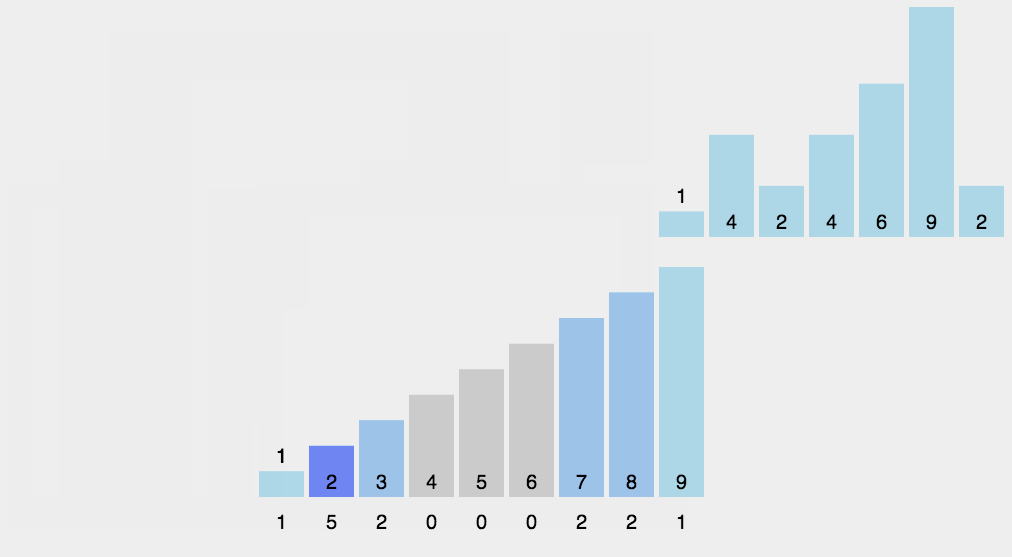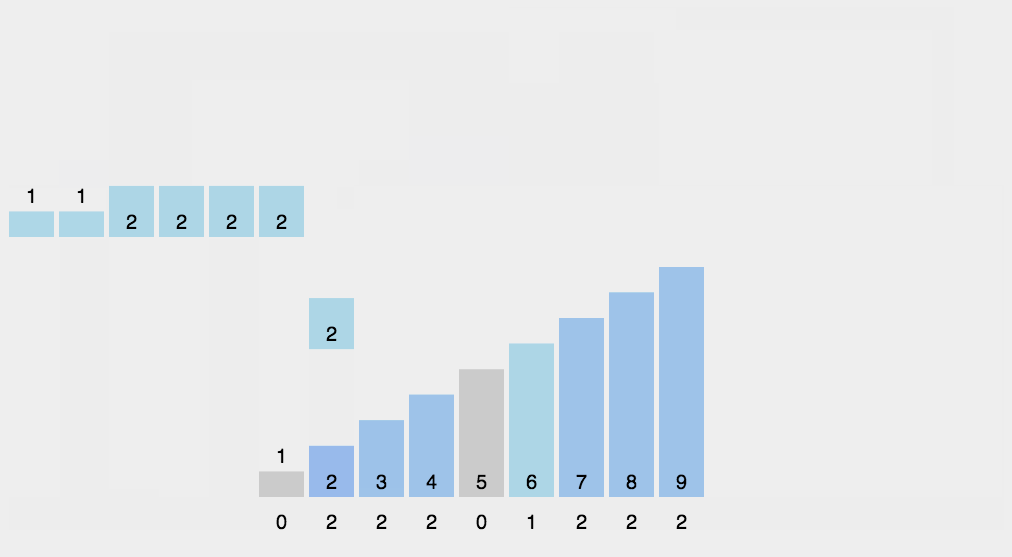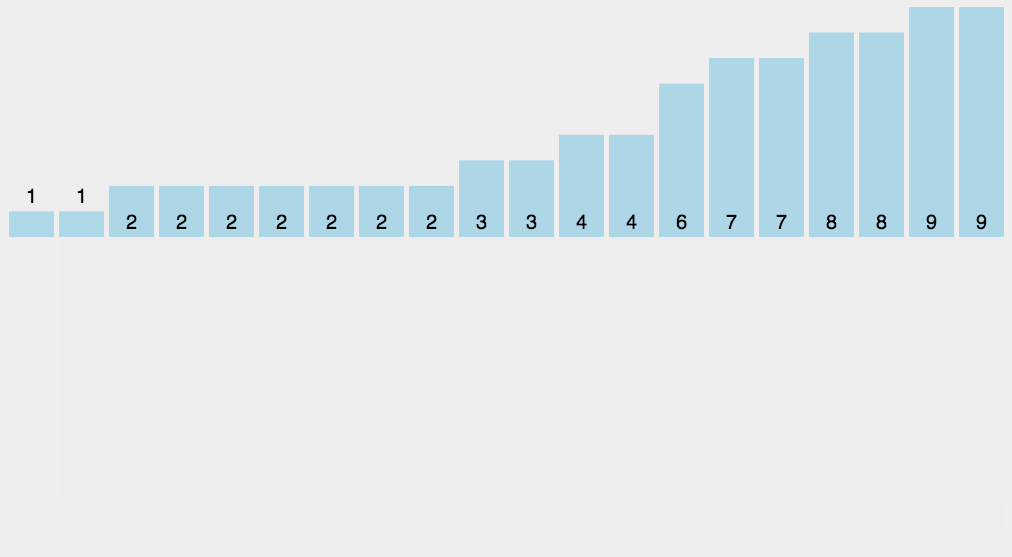
桶排序

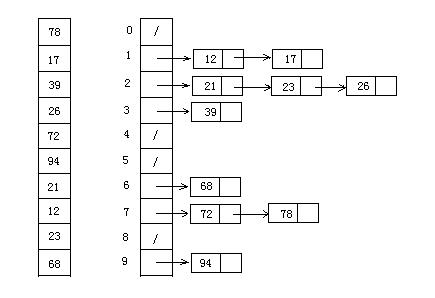
代码

void bucket_sort()
{
    for (int i = 0; i < n; i ++ ) s[q[i]] ++ ;
    for (int i = 1; i < N; i ++ ) s[i] += s[i - 1];
    for (int i = n - 1; i > = 0; i -- ) w[ -- s[q[i]]] = q[i];
    for (int i = 0; i < n; i ++ ) q[i] = w[i];
}

算法分析
桶排序最好情况下使用线性时间 $O(n)$，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为 $O(n)$。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

基数排序

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

图示

代码

void radix_sort(int d, int r)
{
    int radix = 1;
    for (int i = 1; i <= d; i ++ )
    {
        for (int j = 0; j < r; j ++ ) s[j] = 0;
        for (int j = 0; j < n; j ++ ) s[q[j] / radix % r] ++ ;
        for (int j = 1; j < r; j ++ ) s[j] += s[j - 1];
        for (int j = n - 1; j >= 0; j -- ) w[ -- s[q[j] / radix % r]] = q[j];
        for (int j = 0; j < n; j ++ ) q[j] = w[j];
        radix *= r;
    }
}

题解 - yxc版本

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
int q[N], sz, w[N];

void insert_sort()  // 直接插入排序
{
    for (int i = 1; i < n; i ++ )
    {
        int t = q[i], j = i;
        while (j && q[j - 1] > t)
        {
            q[j] = q[j - 1];
            j -- ;
        }
        q[j] = t;
    }
}

void binary_search_insert_sort()  // 折半插入排序
{
    for (int i = 1; i < n; i ++ )
    {
        if (q[i - 1] <= q[i]) continue;
        int t = q[i];
        int l = 0, r = i - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (q[mid] > t) r = mid;
            else l = mid + 1;
        }
        for (int j = i - 1; j >= r; j -- )
            q[j + 1] = q[j];
        q[r] = t;
    }
}

void bubble_sort()  // 冒泡排序
{
    for (int i = 0; i < n - 1; i ++ )
    {
        bool has_swap = false;
        for (int j = n - 1; j > i; j -- )
            if (q[j] < q[j - 1])
            {
                swap(q[j], q[j - 1]);
                has_swap = true;
            }
        if (!has_swap) break;
    }
}

void select_sort()  // 简单选择排序
{
    for (int i = 0; i < n - 1; i ++ )
    {
        int k = i;
        for (int j = i + 1; j < n; j ++ )
            if (q[j] < q[k])
                k = j;
        swap(q[i], q[k]);
    }
}

void shell_sort()  // 希尔排序
{
    for (int d = n / 3; d; d = d == 2 ? 1 : d / 3)
    {
        for (int start = 0; start < d; start ++ )
        {
            for (int i = start + d; i < n; i += d)
            {
                int t = q[i], j = i;
                while (j > start && q[j - d] > t)
                {
                    q[j] = q[j - d];
                    j -= d;
                }
                q[j] = t;
            }
        }
    }
}

void quick_sort(int l, int r)  // 快速排序
{
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[(l + r) / 2];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(l, j);
    quick_sort(j + 1, r);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= sz && q[u * 2] > q[t]) t = u * 2;
    if (u * 2 + 1 <= sz && q[u * 2 + 1] > q[t]) t = u * 2 + 1;

    if (u != t)
    {
        swap(q[u], q[t]);
        down(t);
    }
}

void heap_sort()  // 堆排序，下标一定要从1开始
{
    sz = n;
    for (int i = n / 2; i; i -- ) down(i);

    for (int i = 0; i < n - 1; i ++ )
    {
        swap(q[1], q[sz]);
        sz -- ;
        down(1);
    }
}

void merge_sort(int l, int r)
{
    if (l >= r) return;
    int mid = l + r >> 1;
    merge_sort(l, mid), merge_sort(mid + 1, r);
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) w[k ++ ] = q[i ++ ];
        else w[k ++ ] = q[j ++ ];
    while (i <= mid) w[k ++ ] = q[i ++ ];
    while (j <= r) w[k ++ ] = q[j ++ ];
    for (i = l, j = 0; j < k; i ++, j ++ ) q[i] = w[j];
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    // insert_sort();
    // binary_search_insert_sort();
    // bubble_sort();
    // select_sort();
    // shell_sort();
    // quick_sort(0, n - 1);
    // heap_sort();
    merge_sort(0, n - 1);


    for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
    return 0;
}

桶排序、基数排序

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1000010;

int n;
int q[N], w[N], s[N];

void bucket_sort()
{
    for (int i = 0; i < n; i ++ ) s[q[i]] ++ ;
    for (int i = 1; i < N; i ++ ) s[i] += s[i - 1];
    for (int i = n - 1; i >= 0; i -- ) w[ -- s[q[i]]] = q[i];
    for (int i = 0; i < n; i ++ ) q[i] = w[i];
}

void radix_sort(int d, int r)
{
    int radix = 1;
    for (int i = 1; i <= d; i ++ )
    {
        for (int j = 0; j < r; j ++ ) s[j] = 0;
        for (int j = 0; j < n; j ++ ) s[q[j] / radix % r] ++ ;
        for (int j = 1; j < r; j ++ ) s[j] += s[j - 1];
        for (int j = n - 1; j >= 0; j -- ) w[ -- s[q[j] / radix % r]] = q[j];
        for (int j = 0; j < n; j ++ ) q[j] = w[j];
        radix *= r;
    }
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    // bucket_sort();
    radix_sort(10, 10);

    for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);

    return 0;
}

参考链接

https://www.cnblogs.com/onepixel/articles/7674659.html